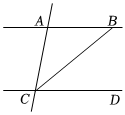
如圖所示，已知∠BAC=100°，CB平分∠ACD．
（1）當添加∠ACD的度數為
80°
80°
時，可判定AB∥CD；
（2）若AB∥CD，則∠ABC的度數為
40°
40°
．
（3）若AB∥CD，在直線CD上取點E，使∠CAE=∠ACB，則∠AEC的度數為
40°或60°
40°或60°
．

【答案】80°；40°；40°或60°

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/6/9 8:30:2組卷：77引用：2難度：0.5

相似題

1．填空并完成以下證明：
如圖，BD⊥AC于點D，EF⊥AC于點F，DM∥BC，∠1=∠2，求證：DM∥GF．
證明：∵BD⊥AC，EF⊥AC（已知）
∴∠BDF=∠EFC=90°（
）
∴BD∥EF（
）
∴∠1=
（兩直線平行，同位角相等）
∵∠1=∠2（已知）
∴∠2=∠HFE（
）
∴GF∥
（內錯角相等，兩直線平行）
∵
∥BC（已知）
∴DM∥GF（如果兩條直線都與第三條直線平行，那么這兩條直線也互相平行）
發布：2025/6/9 14:30:1組卷：382引用：1難度：0.6
解析
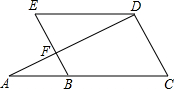2．已知：如圖，∠A=∠ADE，∠C=∠E．
（1）求證：BE∥CD；
（2）若∠EDC=3∠C，求∠C的度數．
發布：2025/6/9 13:0:1組卷：1662引用：14難度：0.5
解析
3．如圖，EF∥AD，∠1=∠2，∠BAC=85°．將求∠AGD的過程填寫完整．
解：∵EF∥AD，
∴∠2=∠3（
）．
又∵∠1=∠2，
∴∠1=∠3（
）．
∴AB∥DG（
）．
∴∠BAC+∠AGD=180°（
）．
∵∠BAC=85°，
∴∠AGD=95°．
發布：2025/6/9 14:0:1組卷：4引用：1難度：0.7
解析

相關試卷

如圖所示，已知∠BAC=100°，CB平分∠ACD．（1）當添加∠ACD的度數為 80°80°時，可判定AB∥CD；（2）若AB∥CD，則∠ABC的度數為 40°40°．（3）若AB∥CD，在直線CD上取點E，使∠CAE=∠ACB，則∠AEC的度數為 40°或60°40°或60°．