已知四邊形ABCD是邊長為1的正方形，點(diǎn)E是射線BC上的動(dòng)點(diǎn)，以AE為直角邊在直線BC的上方作等腰直角三角形AEF，∠AEF=90°，設(shè)BE=m.
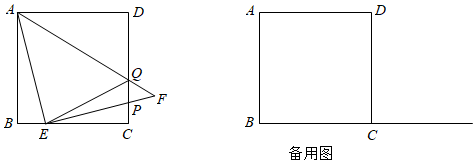
（1）如圖，若點(diǎn)E在線段BC上運(yùn)動(dòng)，EF交CD于點(diǎn)P，AF交CD于點(diǎn)Q，連接CF，
①當(dāng)m=13時(shí)，求線段CF的長；
②在△PQE中，設(shè)邊QE上的高為h,請(qǐng)用含m的代數(shù)式表示h,并求h的最大值；
（2）設(shè)過BC的中點(diǎn)且垂直于BC的直線被等腰直角三角形AEF截得的線段長為y,請(qǐng)直接寫出y與m的關(guān)系式．
1
3
【考點(diǎn)】四邊形綜合題．
【答案】（1）①；
②h=-m2+m，h最大值是；
（2）y=
．
2
3
②h=-m2+m，h最大值是
1
4
（2）y=
1 - 1 2 m - 1 - m 2 （ 1 + m ） + m 2 | （ 0 ≤ m ≤ 1 2 ） |
1 + m 2 2 m 2 + 2 m | （ m ＞ 1 2 ） |
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：3718引用：4難度：0.1
相似題
-
1．【問題發(fā)現(xiàn)】
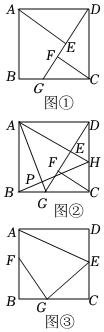
（1）如圖①，在正方形ABCD中，G是BC上一點(diǎn)（點(diǎn)G與B，C不重合），AE⊥DG交DG于點(diǎn)E，CF⊥DG交DG于點(diǎn)F．試猜想線段AE，CF和EF之間的數(shù)量關(guān)系，并證明；
【延伸探究】
（2）在其余條件不變的基礎(chǔ)上延長AE，交DC于點(diǎn)H，連接AG，BH，交于點(diǎn)P，如圖②．求證：AG⊥BH；
【問題解決】
（3）如圖③是一塊邊長為1米的正方形鋼板ABCD．由于磨損，該鋼板的頂點(diǎn)B，C，D均不能使用，王師傅計(jì)劃過點(diǎn)A裁出一個(gè)形如四邊形AEGF的零件，其中點(diǎn)F，E，G分別在AB，CD，BC邊上，且F為AB的中點(diǎn)，GF⊥GE交DC于點(diǎn)E，連接AE，求王師傅能裁出四邊形AEGF的最大面積是多少？發(fā)布：2025/5/23 8:30:2組卷：293引用：2難度：0.3 -
2．問題提出
（1）如圖①，在矩形ABCD的邊BC上找一點(diǎn)E，將矩形沿直線DE折疊，點(diǎn)C的對(duì)應(yīng)點(diǎn)為C′，再在AB上找一點(diǎn)F，將矩形沿直線DF折疊，使點(diǎn)A的對(duì)應(yīng)點(diǎn)A′落在DC上，則∠EDF=．
問題探究
（2）如圖②，在矩形ABCD中，AB=10，AD=4，點(diǎn)P是矩形ABCD邊AB上一點(diǎn)，連接PD、PC，將△ADP、△BCP分別沿PD、PC翻折，得到△A′DP、△B′PC，當(dāng)P、A′、B′三點(diǎn)共線時(shí)，則稱P為AB邊上的“優(yōu)疊點(diǎn)”，求此時(shí)AP的長度．
問題解決
（3）如圖③，矩形ABCD位于平面直角坐標(biāo)系中，AD=4，AD＜AB，點(diǎn)A在原點(diǎn)，B，D分別在x軸與y軸上，點(diǎn)E和點(diǎn)F分別是CD和BC邊上的動(dòng)點(diǎn)，運(yùn)動(dòng)過程中始終保持DE+BF=4．當(dāng)點(diǎn)P是AB邊上唯一的“優(yōu)疊點(diǎn)”時(shí)，連接PE交BD于點(diǎn)M，連接PF交BD于點(diǎn)N，請(qǐng)問DM+BN是否能取得最大值？如果能，請(qǐng)確定此時(shí)點(diǎn)M的位置（即求出點(diǎn)M的坐標(biāo)）及四邊形ADEP的面積，若不能，請(qǐng)說明理由．
發(fā)布：2025/5/23 8:30:2組卷：691引用：1難度：0.1 -
3．綜合與實(shí)踐課上，老師讓同學(xué)們以“矩形的折疊”為主題開展數(shù)學(xué)活動(dòng)．
（1）操作判斷
操作一：對(duì)折矩形紙片ABCD，使AD與BC重合，把紙片展平，得到折痕EF；
操作二：在AD上選一點(diǎn)P，沿BP折疊，使點(diǎn)A落在矩形內(nèi)部點(diǎn)Q處，把紙片展平，連接PQ，BQ．根據(jù)以上操作，當(dāng)點(diǎn)Q在EF上（如圖1）時(shí)，∠QBC=°．
（2）遷移探究
小華將矩形紙片換成正方形紙片，繼續(xù)探究，過程如下：
將正方形紙片ABCD按照（1）中的方式操作，并延長PQ交CD于點(diǎn)G，連接BG．對(duì)角線AC與BP、BG分別交于點(diǎn)M、N，連接PN．當(dāng)點(diǎn)Q在EF上（如圖2）時(shí)，判斷線段PN與BG的位置關(guān)系，并說明理由；
（3）拓展應(yīng)用
在（2）的探究中，改變點(diǎn)P在AD上的位置，當(dāng)點(diǎn)G在線段FC上時(shí)（如圖3），若正方形的邊長為63，求S△BPG的值．，FG=3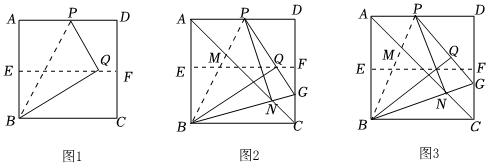
發(fā)布：2025/5/23 8:0:2組卷：358引用：1難度：0.2