通過類比聯(lián)想、引申拓展研究典型題目，可達到解一題知一類的目的．下面是一個案例，請補充完整．
原題：如圖1，點E，F(xiàn)分別在正方形ABCD的邊BC，CD上，∠EAF=45°，連接EF，則EF=BE+DF，試說明理由．
（1）思路梳理
∵AB=CD，∴把△ABE繞點A逆時針旋轉(zhuǎn)90°至△ADG，可使AB與AD重合．∵∠ADC=∠B=90°∠FDG=180°，∴點F，D，G共線．根據(jù) SASSAS（從“SSS，ASA，AAS，SAS”中選擇填寫），易證△AFG≌△AFE△AFE，得EF=BE+DF．
（2）類比引申
如圖2，四邊形ABCD中，AB=AD，∠BAD=90°，點E，F(xiàn)分別在邊BC，CD上，∠EAF=45°．若∠B，∠D都不是直角，則當∠B與∠D滿足等量關(guān)系 ∠B+∠D=180°∠B+∠D=180°時，仍有EF=BE+DF．
（3）聯(lián)想拓展
如圖3，在△ABC中，∠BAC=90°，AB=AC，點D，E均在邊BC上，且∠DAE=45°．猜想BD，DE，EC應(yīng)滿足的等量關(guān)系，并寫出推理過程．
（4）思維深化
如圖4，在△ABC中，∠BAC=60°，AB=AC，點D，E均在直線BC上，點D在點E的左邊，且∠DAE=30°，當AB=4，BD=1時，直接寫出CE的長．
【考點】四邊形綜合題．
【答案】SAS；△AFE；∠B+∠D=180°
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/24 14:0:35組卷：880引用：5難度：0.1
相似題
-
1．數(shù)學(xué)活動課上，老師讓同學(xué)們根據(jù)下面情境提出問題并解答．問題情境：在?ABCD中，點P是邊AD上一點，將△PDC沿直線PC折疊，點D的對應(yīng)點為E．
數(shù)學(xué)思考：
（1）“興趣小組”提出的問題是：如圖1，若點P與點A重合，過點E作EF∥AD，與PC 交于點F，連接DF，則四邊形AEFD是菱形．請你證明“興趣小組”提出的問題；
拓展探究：
（2）“智慧小組”提出的問題是：如圖2，當點P為AD的中點時，延長CE交AB于點F，連接PF．試判斷PF與PC的位置關(guān)系，并說明理由；
問題解決：
（3）“創(chuàng)新小組”在前兩個小組的啟發(fā)下，提出的問題是：如圖3，當點E恰好落在AB邊上時，AP=6，PD=8，DC=20，求AE的長．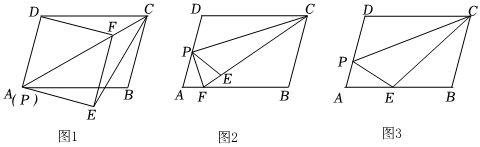
?發(fā)布：2025/5/23 13:0:1組卷：604引用：5難度：0.4 -
2．如圖1，在△ABC中，∠BAC=90°，AB=AC，過點A作AD⊥BC于點D，點M為線段AD上一點（不與A，D重合），在線段BD上取點N，使DM=DN，連接AN，CM．
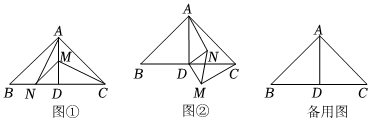
（1）觀察猜想：線段AN與CM的數(shù)量關(guān)系是 ，AN與CM的位置關(guān)系是 ；
（2）類比探究：將△DMN繞點D旋轉(zhuǎn)到如圖2所示的位置，請寫出AN與CM的數(shù)量關(guān)系及位置關(guān)系，并就圖2的情形說明理由；
（3）問題解決：已知AD=3，DM=3，將△DMN繞點D旋轉(zhuǎn)，當以A、D、M、N四點為頂點的四邊形為平行四邊形時，直接寫出BN的長．2發(fā)布：2025/5/23 12:0:2組卷：139引用：3難度：0.1 -
3．綜合與實踐
在綜合實踐課上，同學(xué)們以“正方形的旋轉(zhuǎn)”為主題開展學(xué)習數(shù)學(xué)活動．
操作判斷
（1）操作一：將正方形ABCD與正方形AEFG的頂點A重合，點G在正方形ABCD的邊AD上，如圖1，連接CF，取CF的中點O，連接DO，OG．操作發(fā)現(xiàn)，DO與OG的位置關(guān)系是 ；DO與OG的數(shù)量關(guān)系是 ；
（2）操作二：將正方形AEFG繞頂點A順時針旋轉(zhuǎn)，（1）中的兩個結(jié)論是否仍然成立？如果成立，請僅就圖2的情形進行證明；如果不成立，請說明理由；
拓展應(yīng)用
（3）若AB=4，AE=2，當∠BAG=150°時，請直接寫出DO的長．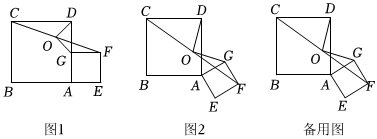
發(fā)布：2025/5/23 11:30:2組卷：456引用：6難度：0.3