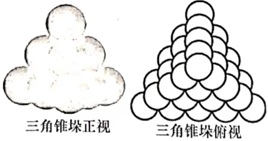
古希臘畢達哥拉斯學(xué)派的“三角形數(shù)”是一列點（或圓球）在等距的排列下可以形成正三角形的數(shù)，如1，3，6，10，15，…，我國宋元時期數(shù)學(xué)家朱世杰在《四元玉鑒》中所記載的“垛積術(shù)”，其中的“落一形”錐垛就是每層為“三角形數(shù)”的三角錐的錐垛（如圖所示，頂上一層1個球，下一層3個球，再下一層6個球…），若一“落一形”三角錐垛有20層，則該錐垛球的總個數(shù)為（ ）
（參考公式：12+22+32+?+n2=n（n+1）（2n+1）6（n∈N*））
1
2
+
2
2
+
3
2
+
?
+
n
2
=
n
（
n
+
1
）
（
2
n
+
1
）
6
（
n
∈
N
*
）
【考點】歸納推理；數(shù)列的求和．
【答案】C
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/5/4 8:0:8組卷：113引用：7難度：0.6
相似題
-
1．按數(shù)列的排列規(guī)律猜想數(shù)列
，23，-45，87，…的第10項是（ ）-169發(fā)布：2024/12/29 13:30:1組卷：105引用：6難度：0.8 -
2．根據(jù)給出的數(shù)塔猜測123456×9+7=（ ）
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…發(fā)布：2024/12/29 11:0:2組卷：545引用：8難度：0.9 -
3．如圖的形狀出現(xiàn)在南宋數(shù)學(xué)家楊輝所著的《詳解九章算法?商功》中，后人稱為“三角垛”．“三角垛”最上層有1個球，第二層有3個球，第三層有6個球，…．設(shè)第n層有an個球，上往下n層球的總數(shù)為Sn，則（ ）發(fā)布：2024/12/29 6:30:1組卷：112引用：7難度：0.7