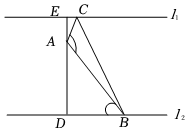
某學校為落實雙減政策，豐富學生的課外活動，計劃在校園內增加室外活動區域（如圖所示△ABC），如圖，已知兩教學樓以直線l1，l2表示，且l1∥l2，ED是過道，A是l1，l2之間的一定點路口，并且點A到l1，l2的距離分別為2，6，B是直線l2上的動點，連接AB，過點A作∠BAC=120°，且使得AC交直線l1于點C（點B，C分別在DE的右側），設∠ABD=α
（1）寫出活動區域△ABC面積S關于角α的函數解析式S（α）；
（2）求函數S（α）的最小值．
【考點】根據實際問題選擇函數類型．
【答案】（1）．
（2）函數S（α）的最小值．
S
（
α
）
=
3
3
sinα
?
cos
（
α
-
30
°
）
（
30
°
＜
α
＜
90
°
）
（2）函數S（α）的最小值
4
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：72引用：3難度：0.5
相似題
-
1．隨著科學技術的發展，放射性同位素技術已經廣泛應用于醫學、航天等眾多領域，并取得了顯著經濟效益．假設某放射性同位素的衰變過程中，其含量P（單位：貝克）與時間t（單位：天）滿足函數關系P（t）=
，其中P0為t=0時該放射性同位素的含量．已知t=15時，該放射性同位素的瞬時變化率為P02-t30，則該放射性同位素含量為4.5貝克時，衰變所需時間為（ ）-32ln210發布：2024/12/29 13:30:1組卷：157引用：11難度：0.7 -
2．隨著“低碳生活，綠色出行”理念的普及，新能源汽車正逐漸成為福清人喜愛的交通工具．據預測，福清某新能源汽車4S店從2023年1月份起的前x個月，顧客對比亞迪汽車的總需量R（x）（單位：輛）與x的關系會近似地滿足
（其中x∈N*且x≤6），該款汽車第x月的進貨單價W（x）（單位：元）與x的近似關系是W（x）=150000+2000x.R（x）=12x（x+1）（39-2x）
（1）由前x個月的總需量R（x），求出第x月的需求量g（x）（單位：輛）與x的函數關系式；
（2）該款汽車每輛的售價為185000元，若不計其他費用，則這個汽車4S店在2023年的第幾個月的月利潤f（x）最大，最大月利潤為多少元？發布：2024/12/29 11:30:2組卷：24引用：3難度：0.5 -
3．某工廠生產某種零件的固定成本為20000元，每生產一個零件要增加投入100元，已知總收入Q（單位：元）關于產量x（單位：個）滿足函數：Q=
．400x-12x2，0≤x≤40080000，x＞400
（1）將利潤P（單位：元）表示為產量x的函數；（總收入=總成本+利潤）
（2）當產量為何值時，零件的單位利潤最大？最大單位利潤是多少元？（單位利潤=利潤÷產量）發布：2024/12/29 13:0:1組卷：234引用：12難度：0.5