對于一個三位數，若其各個數位上的數字都不為0且互不相等，并滿足十位數字最大，個位數字最小，且以各個數位上的數字為三邊可以構成三角形，則稱這樣的三位數為“三角數”．將“三角數”m任意兩個數位上的數字取出組成兩位數，則一共可以得到6個兩位數，其中十位數字大于個位數字的兩位數叫“全數”，十位數字小于個位數字的兩位數叫“善數”，將所有“全數”的和記為Q（m），所有“善數”的和記為S（m），例如：Q（562）=62+52+65=179，S（562）=26+25+56=107；
（1）判斷：342 是是（填“是”或“不是”）“三角數”，572 不是不是（填“是”或“不是”）“三角數”，若是，請分別求出其“全數”和“善數”之和．
（2）若一個正整數a是另一個正整數b的平方，則稱正整數a是完全平方數．若“三角數”n滿足Q（n）-S（n）和Q（n）+S（n）11都是完全平方數，請求出所有滿足條件的n.
Q
（
n
）
+
S
（
n
）
11
【考點】因式分解的應用．
【答案】是；不是
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/7 12:30:2組卷：140引用：1難度：0.9
相似題
-
1．對于一個圖形，通過兩種不同的方法計算它們的面積，可以得到一個數學等式，例如圖1可以得到（a+b）2=a2+2ab+b2，請解答下列問題：
（1）類似圖1的數學等式，寫出圖2表示的數學等式；
（2）若a+b+c=10，ab+ac+bc=35，用上面得到的數學等式乘a2+b2+c2的值；
（3）小明同學用圖3中的x張邊長為a的正方形，y張邊長為b的正方形，z張邊長為a、b的長方形拼出一個面積為（a+7b）（9a+4b）的長方形，求（x+y+z）的值．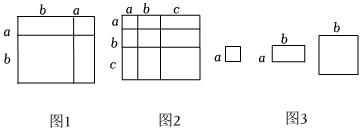
發布：2025/6/7 22:30:2組卷：63引用：2難度：0.6 -
2．利用因式分解進行計算：a（a-b）2-b（b-a）2，其中a=2，
．b=12發布：2025/6/7 22:0:1組卷：23引用：1難度：0.6 -
3．閱讀下列材料，并解答下列問題．
材料一：對于實數x、y,我們將x與y的“優雅數”用f（x,y）來表示，定義為f（x,y）=．xy+3
例如f（2，7）=．27+3=210=15
材料二：對于實數x,用[x]表示不超過實數x的最大整數，即滿足[x]≤x＜[x]+1．
例如：[-1.3]=[-1.74]=-2，[2]=[2.4]=[2.58]=2．
（1）填空：f（4，5）=，[0]=，[-2.3]=．
（2）已知f（x2-2，4）=2，求x的值．
（3）令t=[-y-1]，若|t|=3，求y的取值范圍．23發布：2025/6/7 21:30:1組卷：46引用：2難度：0.5