將小球（看作一點）以速度v1豎直上拋，上升速度隨時間推移逐漸減少直至為0，此時小球達到最大高度，小球相對于拋出點的高度y（m）與時間t（s）的函數解析式為兩部分之和，其中一部分為速度v1（m/s）與時間t（s）的積，另一部分與時間t（s）的平方成正比．若上升的初始速度v1=10m/s,且當t=1s時，小球達到最大高度．
?（1）求小球上升的高度y與時間t的函數關系式（不必寫范圍），并寫出小球上升的最大高度；
（2）如圖，平面直角坐標系中，y軸表示小球相對于拋出點的高度，x軸表示小球距拋出點的水平距離，向上拋出小球時再給小球一個水平向前的均勻速度v2（m/s），發現小球運動的路線為一拋物線，其相對于拋出點的高度y（m）與時間t（s）的函數解析式與（1）中的解析式相同．
①若v2=5m/s,當 t=32s 時，小球的坐標為 （152，154）（152，154），小球上升的最高點坐標為 （5，5）（5，5）；求小球上升的高度y與小球距拋出點的水平距離x之間的函數關系式；
②在小球的正前方的墻上有一高 3536m的小窗戶PQ，其上沿P的坐標為（6，154），若小球恰好能從窗戶中穿過（不包括恰好去中點P，Q，墻厚度不計），請直接寫出小球的水平速度v2的取值范圍．
t
=
3
2
s
15
2
15
4
15
2
15
4
35
36
m
15
4
【考點】二次函數的應用．
【答案】（，）；（5，5）
15
2
15
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：505引用：4難度：0.5
相似題
-
1．如圖，AB，CD是兩個過江電纜的鐵塔，塔高均為40米，AB的中點為P，小麗在距塔底B點西50米的地面E點恰好看到點E，P，C在一直線上，且P，D離江面的垂直高度相等．跨江電纜AC因重力自然下垂近似成拋物線形，為了保證過往船只的安全，電纜AC下垂的最低點距江面的高度不得少于30米．已知塔底B距江面的垂直高度為6米，電纜AC下垂的最低點剛好滿足最低高度要求．
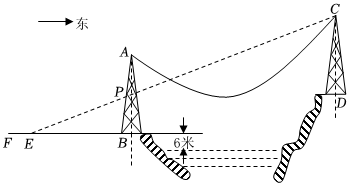
（1）求電纜最低點與河岸EB的垂直高度h及兩鐵塔軸線間的距離（即直線AB和CD之間的水平距離）．
（2）求電纜AC形成的拋物線的二次項系數．發布：2025/5/25 2:0:6組卷：177引用：2難度：0.4 -
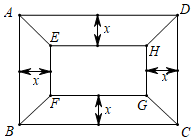2．有一塊矩形地塊ABCD，AB=20米，BC=30米．為美觀，擬種植不同的花卉，如圖所示，將矩形ABCD分割成四個等腰梯形及一個矩形，其中梯形的高相等，均為x米．現決定在等腰梯形AEHD和BCGF中種植甲種花卉；在等腰梯形ABFE和CDHG中種植乙種花卉；在矩形EFGH中種植丙種花卉．甲、乙、丙三種花卉的種植成本分別為20元/米2、60元/米2、40元/米2，設三種花卉的種植總成本為y元．
（1）當x=5時，求種植總成本y；
（2）求種植總成本y與x的函數表達式，并寫出自變量x的取值范圍；
（3）若甲、乙兩種花卉的種植面積之差不超過120平方米，求三種花卉的最低種植總成本．發布：2025/5/25 1:0:1組卷：2658引用：3難度：0.4 -
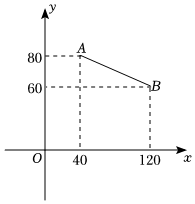3．某時令水果上市的時候，一果農以“線上”與“線下”相結合的方式一共銷售了200箱該種水果．已知“線上”銷售的每箱利潤為50元．“線下”銷售的每箱利潤y（元）與銷售量x（箱）之間的函數關系如圖中線段AB．
（1）若“線上”與“線下”銷售量相同，求果農售完這200箱水果獲得的總利潤；
（2）當“線下”的銷售利潤為4500元時，求“線下”的銷售量；
（3）實際“線下”銷售時，每箱還要支出其它相關費用m元（0＜m＜10），若“線上”與“線下”售完這200箱該水果所獲得的最大總利潤為11225元，求m的值．發布：2025/5/25 1:0:1組卷：143引用：4難度：0.4