數形結合是解決數學問題的一種重要的思想方法，借助圖的直觀性，可以幫助理解數學問題．
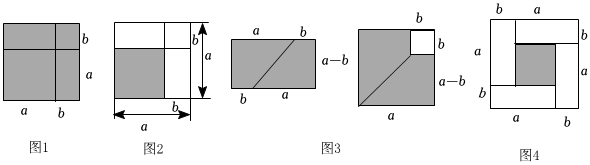
（1）請寫出圖1，圖2，圖3陰影部分的面積分別能解釋的乘法公式．
圖1：（a+b）2=a2+2ab+b2（a+b）2=a2+2ab+b2，圖2：（a-b）2=a2-2ab+b2（a-b）2=a2-2ab+b2，圖3：（a+b）（a-b）=a2-b2（a+b）（a-b）=a2-b2；
（2）用4個全等的長和寬分別為a,b的長方形拼擺成一個如圖4的正方形，請你通過計算陰影部分的面積，直接寫出這三個代數式（a+b）2，（a-b）2，ab之間的等量關系；
（3）根據（1），（2）中你探索發現的結論，完成下列計算：
已知a-b=5，ab=-4，求代數式①a2+b2；②a+b的值．
【考點】完全平方公式的幾何背景．
【答案】（a+b）2=a2+2ab+b2；（a-b）2=a2-2ab+b2；（a+b）（a-b）=a2-b2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/10 9:0:1組卷：872引用：5難度：0.5
相似題
-
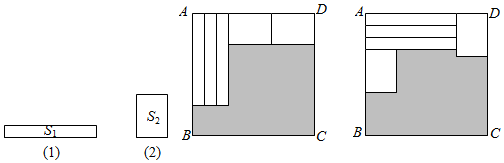
1．如圖，用三個同（1）圖的長方形和兩個同（2）圖的長方形用兩種方式去覆蓋一個大的長方形ABCD，兩種方式未覆蓋的部分（陰影部分）的周長一樣，那么（1）圖中長方形的面積S1與（2）圖中長方形的面積S2的比是 ．
發布：2025/6/13 8:0:2組卷：1720引用：13難度：0.4 -
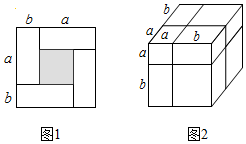2．（1）用兩種不同方法計算同圖形的面積，可以得到一個等式，如圖1，是用長為a,寬為b（a＞b）的四個全等長方形拼成一個大正方形，用兩種不同的方法計算陰影部分（小正方形）的面積，可以得到（a-b）2、（a+b）2、ab三者之間的等量關系式 ．
（2）類似地，用兩種不同的方法計算同一個幾何體的體積，也可以得到一個等式，如圖2，觀察大正方體分割，可以得到等式：．
（3）利用上面所得的結論解答：
①已知x+y=6，xy=5，求x-y的值．
②已知|a+b-5|+（ab-6）2=0，求a3+b3的值．發布：2025/6/12 21:30:1組卷：241引用：3難度：0.6 -
3．用4個長為a,寬為b的長方形拼成如圖所示的大正方形，則用這個圖形可以驗證的恒等式是（ ）發布：2025/6/13 7:0:2組卷：1590引用：7難度：0.7