閱讀下列材料，回答問題．
對任意一個三位數n,如果n滿足各個數位上的數字互不相同，且都不為零，那么稱這個數為“相異數”，將一個“相異數”任意兩個數位上的數字對調后可以得到三個不同的新三位數，把這三個新三位數的和與111的商記為F（n）．例如n=123，對調百位與十位上的數字得到213，對調百位與個位上的數字得到321，對調十位與個位上的數字得到132，這三個新三位數的和為213+321+132=666，因為666÷111=6，所以F（123）=6．
（1）計算：F（341）=88，F（625）=1313；
（2）若s,t都是“相異數”，其中s=100x+32，t=150+y,1≤x≤9，1≤y≤9且x,y都是正整數，規定k=F（s）-F（t），當F（s）+F（t）=19時，求k的最小值．
【考點】因式分解的應用．
【答案】8；13
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/11 8:0:9組卷：536引用：2難度：0.3
相似題
-
1．閱讀下列材料：
若a2-2ab+b2=0，則（a-b）2=0．得a=b；
若a2+b2+c2+2ab-2bc-2ca=0，
則（a+b）2-2c（a+b）+c2=0，
[（a+b）-c]2=0，
得a+b=c；
解決下列問題：
（1）若b2=4（ab-a2），證明：b=2a.
（2）若（b-c）2=4（a-b）（c-a），證明：b+c=2a.發布：2025/6/6 16:0:1組卷：827引用：2難度：0.5 -
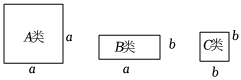2．有如圖所示的A類，B類和C類（a＞b）卡片各4張，從中取出若干卡片，每種卡片至少取一張，把取出的這些卡片拼成一個正方形（無空隙，無重疊拼接），則拼成正方形的邊長最長的可以為（ ）發布：2025/6/6 17:0:1組卷：34引用：1難度：0.5 -
3．已知x-y=5，xy=-3，則代數式x2y-xy2的值為 ．
發布：2025/6/6 16:30:1組卷：330引用：4難度：0.7