設(shè)△ABC的三邊長分別為BC=2，CA=3，AB=4，ha，hb，hc分別表示邊BC、CA、AB上的高，則（ha+hb+hc）（1ha+1hb+1hc）=（ ）
（
h
a
+
h
b
+
h
c
）
（
1
h
a
+
1
h
b
+
1
h
c
）
【考點】三角形的面積．
【答案】B
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/27 22:0:2組卷：223引用：2難度：0.9
相似題
-
1．如圖，D、E分別是△ABC的AC、AB邊上的點，BD、CE相交于點O，若S△OCD=2，S△OBE=3，S△OBC=4，求四邊形ADOE的面積．發(fā)布：2025/5/28 17:30:1組卷：315引用：2難度：0.3 -
2．如圖，在五邊形ABCDE中，BC∥AD，BD∥AE，AB∥EC．圖中與△ABC面積相等的三角形有（ ）發(fā)布：2025/5/28 18:0:1組卷：241引用：2難度：0.9 -
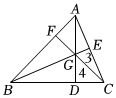3．如圖所示，△ABC中，點D、E、F分別在三邊上，E是AC的中點，AD、BE、CF交于一點G，BD=2DC，S△GEC=3，S△GDC=4，則△ABC的面積是（ ）發(fā)布：2025/5/28 18:0:1組卷：905引用：21難度：0.7
相關(guān)試卷