我們知道：任意一個二元一次方程ax+by=c都有無數個解．現約定：在平面直角坐標系中，不妨將二元一次方程ax+by=c每一個解用一個點表示出來，記為G（x,y），稱G（x,y）為“關聯點”；將這些“關聯點”在坐標系中連接便可得到一條直線，稱這條直線為“關聯點”的“關聯線”．根據所學，解決以下問題：
（1）已知A（-3，-2），B（-1，-13），C（1，-43）三個點中，是“關聯線”l：5x-6y=-3的“關聯點”有 A和BA和B（填字母）；
（2）已知D，P兩點是“關聯線”m：5x-6y=-3的“關聯點”，且D在y軸上；E，P兩點是“關聯線”n：11x-6y=27的“關聯點”，且E在y軸上．若在平面直角坐標系中存在一點Q，滿足PQ∥DE且PQ=DE，求點Q的坐標；
（3）在平面直角坐標系xOy中，點F為“關聯線”x-3y=0的“關聯點”．將點F（x,y）經過變換τ得到點G（x′，y′），該變換記作τ（x,y）=（x′，y′），其中x′=ax+by-2 y′=ax-by+1
（a,b為常數），若將點F向左平移2個單位長度，再向上平移1個單位長度后能與點G重合，求a-b的值．
1
3
4
3
x ′ = ax + by - 2 |
y ′ = ax - by + 1 |
【考點】一次函數綜合題．
【答案】A和B
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：738引用：2難度：0.3
相似題
-
1．已知：如圖1，在平面直角坐標系中，一次函數y=
x+3交x軸于點A，交y軸于點B，點C是點A關于y軸對稱的點，過點C作y軸平行的射線CD，交直線AB與點D，點P是射線CD上的一個動點．34
（1）求點A，B的坐標．
（2）如圖2，將△ACP沿著AP翻折，當點C的對應點C′落在直線AB上時，求點P的坐標．
（3）若直線OP與直線AD有交點，不妨設交點為Q（不與點D重合），連接CQ，是否存在點P，使得S△CPQ=2S△DPQ，若存在，請求出對應的點Q坐標；若不存在，請說明理由．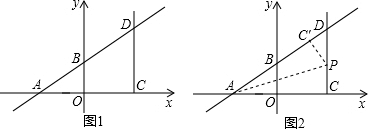
發布：2025/6/9 21:0:1組卷：5624引用：9難度：0.1 -
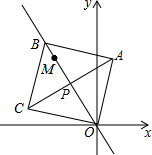2．如圖，點M（-3，4），點P從O點出發，沿射線OM方向1個單位/秒勻速運動，運動的過程中以P為對稱中心，O為一個頂點作正方形OABC，當正方形面積為128時，點A坐標是（ ）發布：2025/6/9 22:0:2組卷：3720引用：9難度：0.3 -
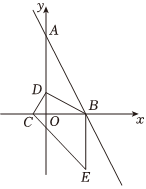3．如圖，直線AB：y=-x+9交y軸于A，交x軸于B，x軸上一點C（-1，0），D為y軸上一動點，把線段BD繞B點逆時針旋轉120°得到線段BE，連接CE，CD，則當CE長度最小時，線段CD的長為（ ）95發布：2025/6/9 22:30:2組卷：3811引用：4難度：0.1