在Rt△ABC中，∠ACB=90°，AC=BC=1，點Q在直線BC上，且AQ=2，則線段BQ的長為（ ）
【考點】等腰直角三角形．
【答案】C
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/7/9 8:0:8組卷：693引用：12難度：0.6
相似題
-
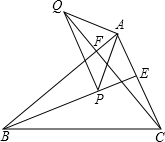1．如圖，已知△ABC中，AB＞AC，BE、CF都是△ABC的高，P是BE上一點且BP=AC，Q是CF延長線上一點且CQ=AB，連接AP、AQ、QP，判斷△APQ的形狀．發(fā)布：2025/5/29 8:30:1組卷：723引用：2難度：0.3 -
2．如圖，△ABC是等腰三角形，∠C=90°，O是△ABC內一點，點O到△ABC各邊的距離等于1，將△ABC繞點O順時針旋轉45°得到△A1B1C1，兩三角形的公共部分為多邊形KLMNPQ．
①證明：△AKL，△BMN，△CPQ都是等腰直角三角形．
②求△ABC與△A1B1C1公共部分的面積．發(fā)布：2025/5/29 9:0:1組卷：42引用：4難度：0.3 -
3．如圖，在等腰Rt△ABC的斜邊AB上取兩點M，N，使∠MCN=45°，記AM=m,MN=n,BN=x,則以線段x、m、n為邊長的三角形的形狀是（ ）發(fā)布：2025/5/29 2:0:5組卷：787引用：7難度：0.5