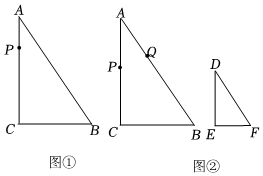
如圖，在Rt△ABC中，∠C=90°，BC=6cm,AC=8cm,AB=10cm.現有一動點P，從點A出發，沿著三角形的邊AC→CB→BA運動，回到點A停止，速度為2cm/s.設運動時間為t s.
（1）當0≤t≤4時，AP=2t cm2t cm；當7≤t≤12時，AP=（24-2t）cm（24-2t）cm；
（2）如圖①，當t=112s或192s112s或192s時，△APC的面積等于△ABC面積的一半；
（3）如圖②，在△DEF中，∠E=90°，DE=4cm,DF=5cm,∠D=∠A．在△ABC的邊上，若另外有一個動點Q，與點P同時從點A出發，沿著邊AB→BC→CA運動，回到點A停止．在兩點運動過程中的某一時刻，恰好△APQ與△DEF全等，請直接寫出點Q的運動速度．
11
2
19
2
11
2
19
2
【考點】三角形綜合題．
【答案】2t cm；（24-2t）cm；s或s
11
2
19
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/19 8:0:9組卷：350引用：1難度：0.3
相似題
-
1．在△ABC中，AB=AC，點D是直線BC上一點（不與B、C重合），以AD為一邊在AD的右側作△ADE，使AD=AE，∠DAE=∠BAC，連接CE．
（1）如圖1，當點D在線段BC上，如果∠BAC=90°，則∠BCE=度；
（2）如圖2，當點D在線段BC上，如果∠BAC=60°，則∠BCE=度；
（3）設∠BAC=α，∠BCE=β
①如圖3，當點D在線段BC上移動，則α，β之間有怎樣的數量關系？請說明理由；
②當點D在直線BC上移動，請直接寫出α，β之間的數量關系，不用證明．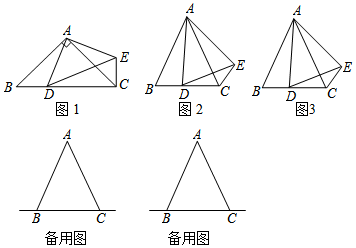
發布：2025/6/9 13:0:1組卷：632引用：7難度：0.3 -
2．感知發現：（1）在學習平行線中，興趣小組發現了很多有趣的模型圖，如圖1，當AB∥CD時，可以得到結論：∠BED=∠B+∠D．在學習逆命題時，發現原命題是真命題，逆命題不一定是真命題，于是興趣小組想嘗試證明：如圖1，∠BED=∠B+∠D，求證：AB∥CD．請寫出證明過程．
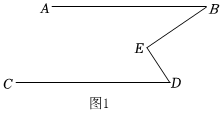
利用這個“模型結論”，我們可以解決很多問題：
綜合與實踐，（2）在綜合與實踐課上，同學們以“一個含30°角的直角三角尺和兩條平行線”為背景開展數學活動，如圖2．已知兩直線a,b且a∥b和直角三角形ABC，∠BCA=90°，∠BAC=30°，∠ABC=60°．創新小組的同學發現∠2-∠1=120°，說明理由．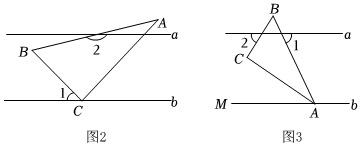
實踐探究：（3）縝密小組在創新小組發現結論的基礎上，將圖2中的圖形繼續變化得到圖3，AC平分∠BAM，此時發現∠1與∠2又存在新的數量關系，請直接寫出答案．發布：2025/6/9 11:30:1組卷：317引用：1難度：0.2 -
3．已知AB∥CD，點M、N分別是AB、CD上兩點，點G在AB、CD之間，MB．
（1）如圖1，若GM⊥GN，求∠AMG+∠CNG的度數：
（2）如圖2，若點P是CD下方一點，MG平分∠BMP，ND平分∠GNP，已知∠BMG=32°，求∠MGN+∠MPN的度數；
（3）如圖3，若點E是AB上方一點，連接EM、EN，且GM的延長線MF平分∠AME，NE平分∠CNG，2∠MEN+∠MGN=105°，求∠AME的度數．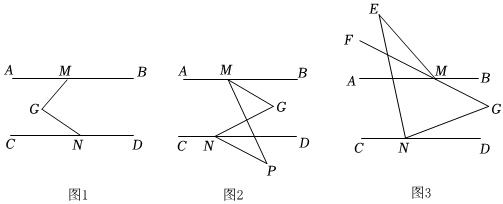
發布：2025/6/9 11:30:1組卷：164引用：1難度：0.3