感知發(fā)現(xiàn)：（1）在學(xué)習(xí)平行線中，興趣小組發(fā)現(xiàn)了很多有趣的模型圖，如圖1，當(dāng)AB∥CD時，可以得到結(jié)論：∠BED=∠B+∠D．在學(xué)習(xí)逆命題時，發(fā)現(xiàn)原命題是真命題，逆命題不一定是真命題，于是興趣小組想嘗試證明：如圖1，∠BED=∠B+∠D，求證：AB∥CD．請寫出證明過程．
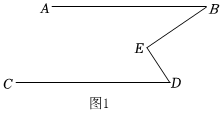
利用這個“模型結(jié)論”，我們可以解決很多問題：
綜合與實踐，（2）在綜合與實踐課上，同學(xué)們以“一個含30°角的直角三角尺和兩條平行線”為背景開展數(shù)學(xué)活動，如圖2．已知兩直線a,b且a∥b和直角三角形ABC，∠BCA=90°，∠BAC=30°，∠ABC=60°．創(chuàng)新小組的同學(xué)發(fā)現(xiàn)∠2-∠1=120°，說明理由．
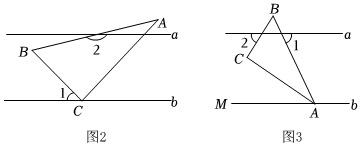
實踐探究：（3）縝密小組在創(chuàng)新小組發(fā)現(xiàn)結(jié)論的基礎(chǔ)上，將圖2中的圖形繼續(xù)變化得到圖3，AC平分∠BAM，此時發(fā)現(xiàn)∠1與∠2又存在新的數(shù)量關(guān)系，請直接寫出答案．
【考點】三角形綜合題．
【答案】（1）（2）證明見解析部分；
（2）∠2+∠1=90°．理由見解析部分．
（2）∠2+
1
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/9 11:30:1組卷：317引用：1難度：0.2
相似題
-
1．綜合與實踐
問題情境：數(shù)學(xué)活動課上，王老師出示了一個問題：
如圖1，在△ABC中，D在AB邊上，E在AC邊上，BE與CD相交于點F，∠A=∠EBC+∠DCB．
求證∠A+∠DFE=180°．
獨立思考：（1）請解答王老師提出的問題．
實踐探究：（2）在原有問題條件不變的情況下，王老師增加下面的條件，并提出新問題，請你解答．
“如圖2，若AB=AC．猜想線段BE與線段CD的數(shù)量關(guān)系，并證明．”
問題解決：（3）數(shù)學(xué)活動小組同學(xué)對上述問題進行研究之后發(fā)現(xiàn)，當(dāng)AE=EF時，若給出圖2中任意兩邊長，則圖2中所有已經(jīng)用字母標記的線段長均可求．該小組提出下面的問題，請你解答．
“如圖3，在（2）的條件下，若AE=EF=2，EC=3，求AD的長．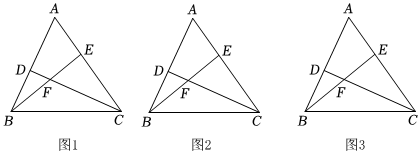
發(fā)布：2025/6/9 14:30:1組卷：125引用：1難度：0.1 -
2．在Rt△ABC中，∠C=90°，AC=4，BC=3，動點P從點A出發(fā)，以每秒4個單位長度的速度向終點B運動．過點P作PQ⊥AB交折線AC-CB于點Q，作點C關(guān)于直線PQ的對稱點C'．設(shè)點P的運動時間為t（t＞0）．
（1）用含t的代數(shù)式表示線段PQ的長；
（2）當(dāng)點Q在線段AC上時，設(shè)直線PQ與直線BC交于點M，當(dāng)△APQ和△QCM全等時，求t的值；
（3）當(dāng)△PCC'為等邊三角形時，直接寫出滿足條件的t值；
（4）當(dāng)點C'和△ABC的某兩個頂點距離相等時，直接寫出滿足條件的t值．發(fā)布：2025/6/9 16:0:2組卷：111引用：1難度：0.2 -
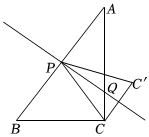
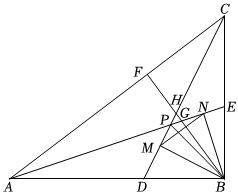3．如圖，在直角三角形ABC中，∠ABC=90°，AB=8，BC=6，∠CAB和∠ACB的角平分線AE，CD交于點P，AC邊上的高BF與AE、CD分別交于點G、H，M、N分別為DH、EG的中點，連接MN、BM、BN，下列說法正確的是 ．
①BF=4.8，
②△ABP與△CBP的面積之比為3：4，
③△BDH為等腰三角形，
④BN⊥AE，
⑤∠MNP=∠EAB（請?zhí)钊胂鄳?yīng)的序號）．發(fā)布：2025/6/9 16:0:2組卷：160引用：1難度：0.4