為了測量學校旗桿（垂直于水平地面）的高度，班里三個興趣小組設計了三種不同的測量方案，如下表所示．
| 課題 | 測量校園旗桿的高度 | ||
| 測量工具 | 測角儀（測量角度的儀器），卷尺，平面鏡等 | ||
| 測量小組 | A組 | B組 | C組 |
| 測量方案示意圖 |
|
|
|
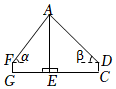
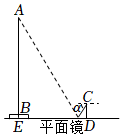
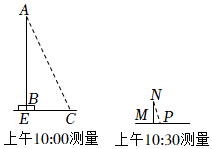
| 說明 | 線段AB表示旗桿的高度，線段BE表示旗桿底座高度，點A，B，E共線，線段CD，FG表示測角儀的高度，點A，B，C，D，E，F，G在同一豎直平面內，CG表示兩次測角儀擺放位置的距離，測角儀可測得旗桿頂端A的仰角 | 線段AB表示旗桿的高度，線段BE表示旗桿底座高度，點A，B，E共線，線段CD表示測角儀的高度，DE表示測角儀到旗桿的距離，點F表示平面鏡的中心，點E，F，D共線，眼睛在C處，移動平面鏡，看向中心F，恰好看到旗桿頂端A，此時用測角儀測得平面鏡的俯角，A，B，C，D，E，F六點在同一豎直平面內 | 線段AB表示旗桿的高度，線段BE表示旗桿底座高度，點A，B，E共線，EC為旗桿與底座某一時刻下的影長，A，B，C，E四點在同一豎直平面內，標桿NM垂直于水平地面，PM為標桿NM在某一時刻的影長 |
| 測量數據 | α為53°，β為45°，CD=FG=1.5米，BE=0.5米，CG=14.79米 | DE=6.61米，CD=1.5米，BE=0.5米，α為60° | CE=4.66米，MN=1米，MP=0.21米，BE=0.5米 |
（2）請結合所學知識，利用A組測量的數據計算出旗桿的高度AB．（結果保留兩位小數．參考數據：
tan
53
°≈
4
3
3
≈
1
.
732
【考點】解直角三角形的應用-仰角俯角問題；平行投影．
【答案】（1）C小組測量的數據計算出的旗桿高度不是旗桿的真實高度，因為C小組測量的CE和PM不是同一時刻的兩物體的影長；
（2）旗桿的高度AB約為9.45m．
（2）旗桿的高度AB約為9.45m．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/23 16:0:1組卷：182引用：3難度：0.6
相似題
-
1．如圖，某學習小組在教學樓AB的頂部觀測信號塔CD底部的俯角為30°，信號塔頂部的仰角為45°．已知教學樓AB的高度為20m,求信號塔的高度（計算結果保留根號）．發布：2025/5/24 0:0:1組卷：844引用：6難度：0.6 -
2．為了落實雙減政策，學校開展了豐富多彩的興趣活動．周末數學組王老師帶領興趣小組學生到校外搞測量．如圖，大樓AB右側有一障礙物，在障礙物的旁邊有一幢小樓DE，在小樓的頂端D處測得障礙物邊緣點C的俯角為30°，測得大樓頂端A的仰角為45°（點B、C、E在同一水平直線上），測得AB=40m,DE=5m,聰明的同學，請你求障礙物B、C兩點間的距離．發布：2025/5/24 0:0:1組卷：130引用：1難度：0.5 -
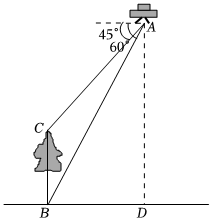3．學校玩轉數學小組利用無人機測量大樹BC的高，當無機在A處時，恰好測得大樹頂端C的俯角為45°，大樹底端B的俯角為60°，此時無人機距離地面的高度AD=30米，求大樹BC的高．（結果保留小數點后一位．，2=1.414）3=1.732發布：2025/5/24 1:0:1組卷：115引用：1難度：0.6