如圖，矩形EFGH內接于△ABC（矩形各頂點在三角形邊上），E，F在BC上，H，G分別在AB，AC上，且AD⊥BC于點D，交HG于點N．
（1）求證：△AHG∽△ABC；
（2）若AD=3，BC=9，設EH=x,矩形EFGH的面積為y,求出y與x之間的函數表達式，并寫出自變量x的取值范圍．
【考點】相似三角形的判定與性質；函數關系式．
【答案】（1）見證明過程；
（2）y=-3x2+9x（0＜x＜3）．
（2）y=-3x2+9x（0＜x＜3）．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/19 15:0:1組卷：1539引用：5難度：0.5
相似題
-
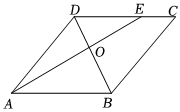1．如圖，在菱形ABCD中，E為邊CD上一點，AE、BD交于點O．若S△DOE：S△BOA=4：9，則CE：AD等于（ ）發布：2025/5/30 14:0:1組卷：179引用：3難度：0.6 -
2．如圖所示，等邊三角形ABC的邊長為3，P為BC上一點，且BP=1，D為AC上一點，若∠APD=60°，求CD的長．發布：2025/5/30 14:0:1組卷：797引用：6難度：0.3 -
3．【閱讀理解】小白同學遇到這樣一個問題：
△ABC中，D是BC的中點，E是AB上一點，延長DE、AC交于點F，DE=EF，AB=5，求AE的長．
小白的想法是：過點E作EH∥BC交AC于H，再通過相似三角形的性質得到AE、BE的比，從而得出AE的長，請你按照小白的思路完成解答．
【解決問題】請借助小白的解題經驗，完成下面問題：
△ABC中，AD平分∠BAC交BC于D，E為AB邊上一點，AE=AD，H、Q為BC上兩點，CQ=DH，DQ=mDH，G為AC上一點，連接EQ交HG、AD于F、P，∠EFG+∠EAD=180°，猜想并驗證EP與GH的數量關系．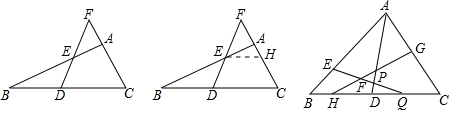
發布：2025/5/30 14:0:1組卷：1553引用：3難度：0.4