如圖，在等腰Rt△ABC中，∠ABC=90°，AB=BC，點D在線段BC的中垂線上，連接BD、CD．
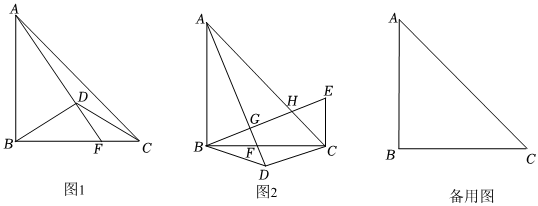（1）如圖1，若∠BDC=120°時，連接AD并延長交BC于點F，若AB=6，求△ACD的面積；
（2）如圖2，連接AD，若∠ADC=90°，過點B作BE⊥AD于點G，交AC于點H，過點C作CE⊥BC交BH的延長線于點E．求證：EH+DF=2BG；
（3）在等腰Rt△ABC內(nèi)部有一點P，連接PA、PB、PC，將△ABP沿直線AB翻折至△ABP所在平面內(nèi)得到△ABQ，連接CQ，當(dāng)12PA+PB+52PC取得最小值時，請直接寫出CQBC的值．
EH
+
DF
=
2
BG
1
2
PA
+
PB
+
5
2
PC
CQ
BC
【考點】相似形綜合題．
【答案】（1）9-3；
（2）證明見解答觀察；
（3）=．
3
（2）證明見解答觀察；
（3）
CQ
BC
170
10
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/5/2 8:0:9組卷：824引用：3難度：0.1
相似題
-
1．小波在復(fù)習(xí)時，遇到一個課本上的問題，溫故后進(jìn)行了操作、推理與拓展．
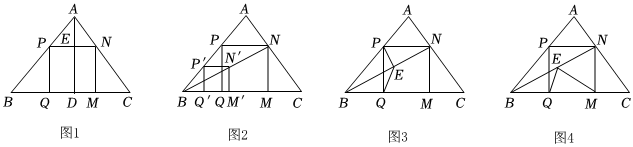
（1）溫故：如圖1，在△ABC中，AD⊥BC于點D，正方形PQMN的邊QM在BC上，頂點P，N分別在AB，AC上，且．若BC=6，AD=4，則正方形PQMN的邊長等于 ；PNBC+MNAD=1
（2）操作：能畫出這類正方形嗎？小波按數(shù)學(xué)家波利亞在《怎樣解題》中的方法進(jìn)行操作：如圖2，任意畫△ABC，在AB上任取一點P'，畫正方形P'Q'M'N'，使Q'，M'在BC邊上，N'在△ABC內(nèi)，連結(jié)BN'并延長交AC于點N，畫NM⊥BC于點M，NP⊥NM交AB于點P，PQ⊥BC于點Q，得到四邊形PQMN；
（3）推理：如圖3，若點E是BN的中點，求證：EP=EQ；
（4）拓展：在（2）的條件下，射線BN上截取NE=NM，連結(jié)EQ，EM（如圖4）．當(dāng)∠NBM=30°時，猜想∠QEM的度數(shù)，并嘗試證明．
請幫助小波解決“溫故”、“推理”、“拓展”中的問題．發(fā)布：2025/6/7 9:0:2組卷：103引用：3難度：0.3 -
2．問題背景：如圖（1），在矩形ABCD中，過C作CE⊥BD于F，交AD于E，圖中與△ABD相似的三角形有多個，試寫出其中一個三角形并證明．
嘗試運用：如圖（2），在四邊形ABCD中，∠A=∠B=90°，點E為AB上一點，過點E作EF⊥CD交CD的延長線于點F，交AD于點G，求證：EG?AB=CD?AG．
拓展創(chuàng)新：如圖（3），在四邊形ABCD中，∠BAD=∠BCD=90°，BA=BC=1，DA=DC=3，點E，F(xiàn)分別在邊AB，AD上，連接DE，CF．若DE⊥CF，求的值．DECF
發(fā)布：2025/6/9 8:30:2組卷：808引用：2難度：0.1 -
3．如圖①，在Rt△ABC中，∠C=90°，BC=8cm,AC=6cm,點P由A點出發(fā)以1cm/s的速度向終點C勻速移動，同時點Q由點C出發(fā)以2cm/s的速度向終點B勻速移動，當(dāng)一個點到達(dá)終點時另一個點也隨之停止移動．
（1）填空：在 秒時，△PCQ的面積為△ACB的面積的；38
（2）經(jīng)過幾秒，以P、C、Q為頂點的三角形與△ACB相似？
（3）如圖②，D為AB上一點，且AD=AC，運動時間t為多少時，CD⊥PQ？發(fā)布：2025/6/9 4:30:2組卷：133引用：2難度：0.3
相關(guān)試卷