小波在復習時，遇到一個課本上的問題，溫故后進行了操作、推理與拓展．
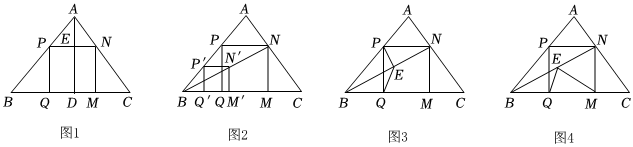
（1）溫故：如圖1，在△ABC中，AD⊥BC于點D，正方形PQMN的邊QM在BC上，頂點P，N分別在AB，AC上，且PNBC+MNAD=1．若BC=6，AD=4，則正方形PQMN的邊長等于 125125；
（2）操作：能畫出這類正方形嗎？小波按數學家波利亞在《怎樣解題》中的方法進行操作：如圖2，任意畫△ABC，在AB上任取一點P'，畫正方形P'Q'M'N'，使Q'，M'在BC邊上，N'在△ABC內，連結BN'并延長交AC于點N，畫NM⊥BC于點M，NP⊥NM交AB于點P，PQ⊥BC于點Q，得到四邊形PQMN；
（3）推理：如圖3，若點E是BN的中點，求證：EP=EQ；
（4）拓展：在（2）的條件下，射線BN上截取NE=NM，連結EQ，EM（如圖4）．當∠NBM=30°時，猜想∠QEM的度數，并嘗試證明．
請幫助小波解決“溫故”、“推理”、“拓展”中的問題．
PN
BC
+
MN
AD
=
1
12
5
12
5
【考點】相似形綜合題．
【答案】
12
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：103引用：3難度：0.3
相似題
-
1．【問題情境】
（1）古希臘著名數學家歐幾里得在《幾何原本》提出了射影定理，又稱“歐幾里德定理”：在直角三角形中，斜邊上的高是兩條直角邊在斜邊射影的比例中項，每一條直角邊又是這條直角邊在斜邊上的射影和斜邊的比例中項．射影定理是數學圖形計算的重要定理．
其符號語言是：如圖1，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足為D，則：（1）CD2=AD?BD，（2）AC2=AB?AD，（3）BC2=AB?BD；請你證明定理中的結論（3）BC2=AB?BD．
【結論運用】
（2）如圖2，正方形ABCD的邊長為6，點O是對角線AC、BD的交點，點E在CD上，過點C作CF⊥BE，垂足為F，連接OF，
①求證：△BOF∽△BED；
②若BE=2，求OF的長．10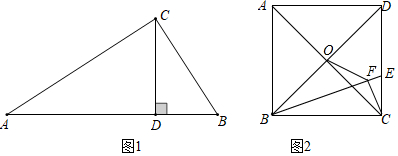
發布：2025/5/22 0:0:2組卷：1315引用：5難度：0.3 -
2．閱讀材料：三角形的三條中線必交于一點，這個交點稱為三角形的重心．
（1）特例感知：如圖（1），已知邊長為2的等邊△ABC的重心為點O，則△OBC的面積為；33
（2）性質探究：如圖（2），已知△ABC的重心為點O，對于任意形狀的△ABC，是不是定值，如果是，請求出定值為多少，如果不是，請說明理由；ODOA
（3）性質應用：如圖（3），在任意矩形ABCD中，點E是CD的中點，連接BE交對角線AC于點M，的值是不是定值，如果是，請求出定值為多少，如果不是，請說明理由；S矩形ABCDS三角形CME
（4）思維拓展：如圖（4），∠MON=30°，N點的坐標為（2，0），M點的坐標為（3，），點Q在線段OM上以每秒1個單位的速度由O向M點移動，當Q運動到M點就停止運動，連接NQ，將△MON分為△OQN和△MQN兩個三角形，當其中一個三角形與原△MON相似時，求點Q運動的時間t.3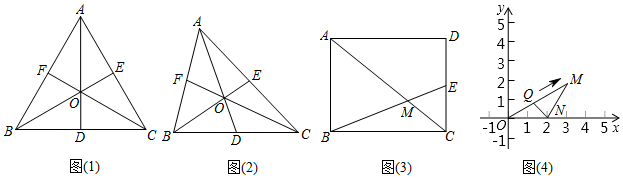
發布：2025/5/22 1:0:1組卷：617引用：4難度：0.1 -
3．如圖，等腰Rt△ABC，∠ACB=90°，分別以AB，AC為邊長在AB同側作等邊△ABD和等邊△ACE，AD與CE相交于點F，連接DE，DC．
（1）求證：BC=DE；
（2）求證：CD2=AC?FC；
（3）已知AB=2，求線段EF的長．發布：2025/5/22 2:30:1組卷：144引用：4難度：0.1