閱讀材料，解決問題
折疊、旋轉(zhuǎn)是我們常見的兩種圖形變化方式如圖1，在Rt△ABC中，∠BAC=90°，AB=AC，點D，E在邊BC上，∠DAE=45°，若BD=3，CE=1，求DE的長．
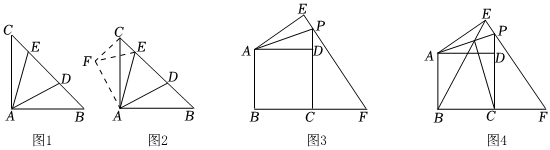
小明發(fā)現(xiàn)，如果將△ABD繞點A按逆時針方向旋轉(zhuǎn)90°，得到△ACF，連接EF（如圖2）．使條件集中在△FCE中，可求得FE（即DE）的長，具體作法為：作AD⊥AF，且AF=AD，連接CF、EF，可證△ACF≌△ABD，再結(jié)合已知中∠DAE=45°，可證△AEF≌△AED，得FE=DE，接著在Rt△FCE中利用勾股定理即可求得FE的長，即ED的長．
（1）請你回答：△AEF與△AED全等的條件是 SASSAS（填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一個），DE的長為 1010；
（2）如圖3，正方形ABCD中，點P為CD延長線上一點，將△ADP沿AP翻折至△AEP位置，延長EP交直線BC于點F．
①求證：BF=EF；
②連接BE交AP于點O，連接CO（如圖4），請你直接寫出BEOC的值．
10
10
BE
OC
【考點】相似形綜合題．
【答案】SAS；
10
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：456引用：3難度：0.2
相似題
-
1．在Rt△ABC中，∠C=90°，AB=10，AC=8，點Q在AB上，且AQ=2，過Q作QR⊥AB，垂足為Q，QR交折線AC-CB于R（如圖1），當(dāng)點Q以每秒2個單位向終點B移動時，點P同時從A出發(fā)，以每秒6個單位的速度沿AB-BC-CA移動，設(shè)移動時間為t秒（如圖2）．
（1）求△BCQ的面積S與t的函數(shù)關(guān)系式．
（2）t為何值時，QP∥AC？
（3）t為何值時，直線QR經(jīng)過點P？
（4）當(dāng)點P在AB上運動時，以PQ為邊在AB上方所作的正方形PQMN在Rt△ABC內(nèi)部，求此時t的取值范圍．發(fā)布：2025/6/10 22:30:2組卷：1843引用：5難度：0.1 -
2．定義：兩個相似等腰三角形，如果它們的底角有一個公共的頂點，那么把這兩個三角形稱為“關(guān)聯(lián)等腰三角形”．如圖，在△ABC與△AED中，BA=BC，EA=ED，且△ABC～AED，所以稱△ABC與△AED為“關(guān)聯(lián)等腰三角形”，設(shè)它們的頂角為α，連接EB，DC，則稱
為“關(guān)聯(lián)比”．DCEB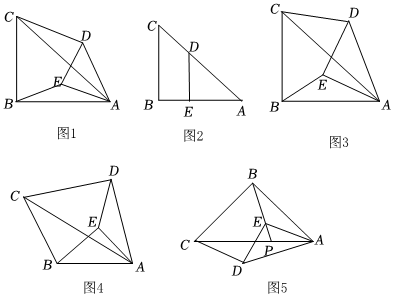
下面是小穎探究“關(guān)聯(lián)比”與α之間的關(guān)系的思維過程，請閱讀后，解答下列問題：
（1）當(dāng)△ABC與△AED為“關(guān)聯(lián)等腰三角形”，且α=90°時，
①在圖2中，若點E落在AB上，則“關(guān)聯(lián)比”=；DCEB
②在圖3中，探究△ABE與△ACD的關(guān)系，并求出“關(guān)聯(lián)比”的值．DCEB
（2）如圖4，當(dāng)△ABC與△AED為“關(guān)聯(lián)等腰三角形”，且α=120°，
①“關(guān)聯(lián)比”=．DCEB
②AB=2時，將△ABC繞點A順時針旋轉(zhuǎn)60°，線段BC掃過的面積是 ．
[遷移運用]
（3）如圖5，△ABC與△AED為“關(guān)聯(lián)等腰三角形”．若∠ABC=∠AED=90°，AC=4，點P為AC邊上一點，且PA=1，點E為PB上一動點，當(dāng)點E自點B運動至點P時，點D所經(jīng)過的路徑長為 ．發(fā)布：2025/6/11 6:0:1組卷：550引用：2難度：0.1 -
3．如圖，在矩形ABCD中，AB=6，BC=4，點M、N分別在AB、AD上，且MN⊥MC，點E為CD的中點，連接BE交MC于點F．
（1）當(dāng)F為BE的中點時，求證：AM=CE；
（2）若=2，求EFBF的值；ANND
（3）若MN∥BE，求的值．ANND發(fā)布：2025/6/10 15:0:1組卷：1654引用：5難度：0.4