2022-2023學年山西省實驗中學九年級（下）第五次月考數學試卷（3月份）

一、單項選擇題

• 1．拋物線y=x²+4x-5的對稱軸為（　　）

  A．y軸

  B．x軸

  C．直線x=2

  D．直線x=-2
  組卷：225引用：2難度：0.6

  解析

• 2．將二次函數y=x²-2x+3變形為頂點式得到的解析式為（　　）

  A．y=（x-1）2+4

  B．y=（x-1）2+2

  C．y=（x+2）2+6

  D．y=（x-2）2+6
  組卷：432引用：2難度：0.7

  解析

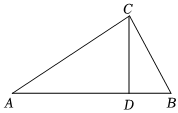• 3．在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足為D，則下列式子中正確的是（　　）

  A． sin A = BC AB

  B． tan A = BC AB

  C． cos B = BD CD

  D． tan B = CD BC
  組卷：81引用：2難度：0.7

  解析

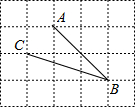• 4．如圖，在網格中，小正方形的邊長均為1，點A，B，C都在格點上，則∠ABC的正切值是（　　）

  A．2

  B． 2 5 5

  C． 5 5

  D． 1 2
  組卷：16972引用：110難度：0.9

  解析

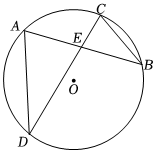• 5．如圖所示，在⊙O中，兩條弦AB、CD相交于點E，連接AD、BC，則下列說法中錯誤的是（　　）

  A．∠A=∠C

  B．∠B=∠D

  C． AE EC = AD BE

  D． AE EC = DE BE
  組卷：71引用：2難度：0.6

  解析

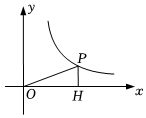• 6．如圖，點P（12，a）在反比例函數

  y

  =

  60

  x

  （

  x

  ＞

  0

  ）

  的圖象上，PH⊥x軸于點H，則cos∠OPH的值為（　　）

  A． 12 13

  B． 5 13

  C． 12 5

  D． 5 12
  組卷：53引用：3難度：0.6

  解析

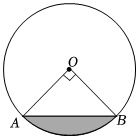• 7．有一只小貓咪隨機的走在如圖所示的圓形地磚上，那么它走在陰影區域上的概率是（　　）（π的值取3）

  A． 1 6

  B． 1 12

  C． 1 8

  D． 1 10
  組卷：142引用：2難度：0.7

  解析

三、解答題

• 22．閱讀材料，解決問題
  折疊、旋轉是我們常見的兩種圖形變化方式如圖1，在Rt△ABC中，∠BAC=90°，AB=AC，點D，E在邊BC上，∠DAE=45°，若BD=3，CE=1，求DE的長．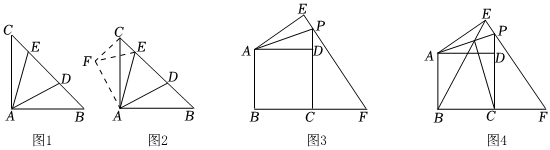
  
  小明發現，如果將△ABD繞點A按逆時針方向旋轉90°，得到△ACF，連接EF（如圖2）．使條件集中在△FCE中，可求得FE（即DE）的長，具體作法為：作AD⊥AF，且AF=AD，連接CF、EF，可證△ACF≌△ABD，再結合已知中∠DAE=45°，可證△AEF≌△AED，得FE=DE，接著在Rt△FCE中利用勾股定理即可求得FE的長，即ED的長．
  （1）請你回答：△AEF與△AED全等的條件是

  （填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一個），DE的長為

  ；
  （2）如圖3，正方形ABCD中，點P為CD延長線上一點，將△ADP沿AP翻折至△AEP位置，延長EP交直線BC于點F．
  ①求證：BF=EF；
  ②連接BE交AP于點O，連接CO（如圖4），請你直接寫出

  BE

  OC

  的值．
  組卷：455引用：3難度：0.2

  解析

• 23．在如圖所示的平面直角坐標系中，拋物線y=-2x²+2x+4與x軸的交點為A、B．與y軸的交點為C．
  
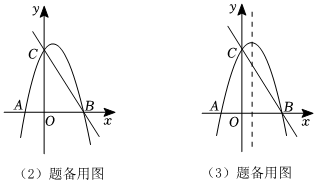
  （1）請你求出點A、B、C的坐標并直接寫出直線BC的關系式；
  （2）若點F是直線BC上方拋物線上的任意一點，連接FB、FC，請你求出△FBC面積的最大值；
  （3）點D在該拋物線的對稱軸上，點E是平面直角坐標系內的任意一點，以點B、C、D、E為頂點的四邊形是矩形，則點E的坐標是

  （請直接寫出答案）．
  組卷：102引用：2難度：0.3

  解析