圖①、圖②、圖③均是5×5的正方形網格，每個小正方形的邊長均為1，每個小正方形的頂點稱為格點，點A、B均在格點上．在圖①、圖②、圖③中，只用無刻度的直尺，在給定的網格中按要求作圖，所畫圖形的頂點均在格點上．
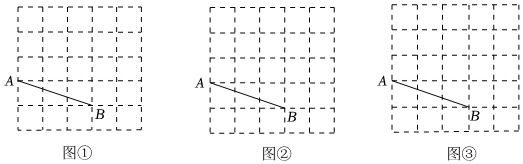
（1）在圖①中，畫等腰三角形ABC，使其面積為3．
（2）在圖②中，畫等腰直角三角形ABD，使其面積為5．
（3）在圖③中，畫平行四邊形ABEF，使∠ABE=135°．
【答案】（1）見解析；
（2）見解析；
（3）見解析．
（2）見解析；
（3）見解析．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/9 21:0:1組卷：194引用：4難度：0.5
相似題
-
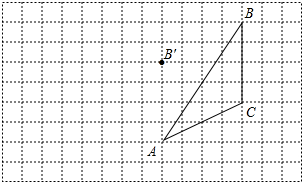1．如圖，每個小正方形的邊長為1，△ABC經過平移得到△A′B′C′．
根據下列條件，利用網格點和直尺畫圖：
（1）補全△A′B′C′；
（2）作出中線CD；
（3）畫出BC邊上的高線AE；
（4）△ABC的面積為．發布：2025/6/10 1:30:1組卷：113引用：4難度：0.5 -
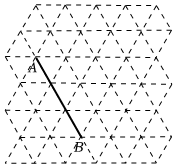2．如圖，等邊三角形網格中，每一個小等邊三角形邊長均為1，A，B在三角形的頂點處，且AB=3，按照要求用無刻度直尺作圖，不要求寫畫法，但是要保留作圖痕跡．（畫圖過程用虛線表示，結果用實線表示）．
（1）過A點作AB的垂線段AC，使其長度為；3
（2）過（1）中的點C作AB的平行線段CD，使其長度為3；
（3）作一個平行四邊形EFGH，使得各邊的中點分別為A，B，C，D（C，D為（2）中的點）．發布：2025/6/9 23:0:1組卷：145引用：3難度：0.6 -
3．問題背景：在△ABC中，AB、BC、AC三邊的長分別為
，5，22，求這個三角形的面積．小明同學在解答這個問題時，先建立一個正方形的網格（每個網格的邊長為1），再在網格中畫出格點△ABC（即△ABC三個頂點都在小正方形的頂點處），如圖1所示，這樣不需求△ABC的高，而借助網格就能直接計算出它的面積．17
（1）請你將△ABC的面積直接填寫在橫線上：．
（2）我們將上速求三角形的面積的方法叫構圖法，若△DEF三邊長分別為，13，29．在圖2中畫出△DEF，并求出它的面積．34
（3）如圖3，已知有一△PQR，分別以PQ，PR為邊向外作正方形PQAF、正方形PRDE，連接EF．若PQ=，PR=22，QR=3，求六邊形AQRDEF的面積．5
發布：2025/6/10 0:30:1組卷：44引用：1難度：0.5