本學期，我們利用“構造軸對稱圖形——等邊三角形”證明了定理：定理在直角三角形中，如果一個銳角等于30°，那么它所對的直角邊等于斜邊的一半．
證明過程如下：
| 已知：如圖1-10（1），△ABC是直角三角形，∠C=90°，∠A=30°．求證：BC= 1 2 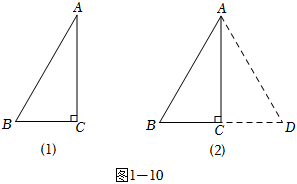 證明：如圖1-10（2），延長BC至點D，使CD=BC，連接AD． ∵∠ACB=90°，∠BAC=30°． ∴∠ACD=90°，∠B=60°． ∵AC=AC， ∴△ABC≌△ADC（SAS）． ∴AB=AD（全等三角形的對應邊相等）． ∴△ABD是等邊三角形（有一個角等于60°的等腰三角形是等邊三 角形）． ∴BC= 1 2 1 2 |
（1）如圖1-10（1），在Rt△ABC中，∠C=90°，若∠A=30°，AB=4，則BC=
2
2
；【類比證明】
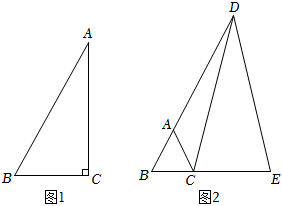
（2）如圖1，請類比以上證明過程，證明：在Rt△ABC中，若∠C=90°，AB=2BC，則∠A=30°；
【遷移創新】
構造具有特殊性質的軸對稱圖形（如等邊三角形），從而利用軸對稱圖形的性質證明結論是幾何問題的數學證明中常見的思路．請你嘗試解決以下問題．
（3）如圖2，等邊△ABC中，延長BA，BC，使AD=BE，連接DC，DE．求證：DC=DE．
【考點】三角形綜合題．
【答案】2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 11:0:1組卷：624引用：4難度：0.5
相似題
-
1．在平面直角坐標系中，O為原點，點A（3，0），點B（0，4），把△ABO繞點B逆時針旋轉，得△A'BO′．點A，O旋轉后的對應點為A'，O'，記旋轉角為α．
（Ⅰ）如圖①，若α=90°，求AA'的長；
（Ⅱ）如圖②．若α=45°，求點O'的坐標；
（Ⅲ）若M為AB邊上的一動點，在OB上取一點N（0，1），將△ABO繞點B逆時針旋轉一周，求MN的取值范圍（直接寫出結果即可）．發布：2025/6/3 17:0:2組卷：687引用：4難度：0.4 -
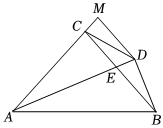2．如圖，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于點E，BD⊥AE于點E，DM⊥AC交AC的延長線于點M，連接CD，下列結論正確的是 ．
①AC+CE=AB；
②為定值；AMAC+AB
③∠CDA=45°；
④．CD=12AE發布：2025/6/3 16:0:1組卷：34引用：1難度：0.3 -
3．【問題】：如圖1，等腰直角三角形ABC中，AB=AC=4，∠BAC=90°，AD是△ABC的角平分線，點E為AD上一點，EF⊥CE交BA延長線于點F，連接CF，探究AE，AC，AF之間的數量關系．
【分析】：小明在思考這道題時，先通過測量猜想出CE=EF，然后他想到了老師講過的“手拉手”模型，便嘗試著過點E作AD的垂線與AC相交于點G（如圖2），通過證明△EAF≌△EGC，最終探究出AE、AC、AF之間的數量關系．
（1）請根據小明的思路，補全△EAF≌EGC的證明過程；
（2）請直接寫出AE，AC，AF之間的數量關系；
【應用】（3）當AF=2時，請直接寫出AE的長為 ；
【拓展】（4）若CF的中點為點M，當B，E，M三點共線時，請直接寫出AE的長為 ．發布：2025/6/3 18:0:1組卷：682引用：1難度：0.4