有5個正整數a1，a2，a3，a4，a5，某數學興趣小組的同學對5個正整數作規律探索，找出同時滿足以下3個條件的數．
①a1，a2，a3是三個連續偶數（a1＜a2＜a3），②a4，a5是兩個連續奇數（a4＜a5），③a1+a2+a3=a4+a5．
該小組成員分別得到一個結論：
甲：取a2=6，5個正整數不滿足上述3個條件；
乙：取a2=12，5個正整數滿足上述3個條件；
丙：當a2滿足“a2是4的倍數”時，5個正整數滿足上述3個條件；
丁：5個正整數a1，a2，a3，a4，a5滿足上述3個條件，則a5=3k+4（k為正整數）；
戊：5個正整數滿足上述3個條件，則a1，a2，a3的平均數與a4，a5的平均數之和是10p（p為正整數）；以上結論正確的個數為 44同學．
【考點】規律型：數字的變化類．
【答案】4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 2:0:7組卷：139引用：1難度：0.4
相似題
-
1．已知a1，a2，…，a2023均為正數，且滿足E=（a1+a2+?+a2022）（a2+a3+?+a2022-a2023），F=（a1+a2+?+a2022-a2023）（a2+a3+?+a2022），則E，F之間的關系是（ ）
發布：2025/6/4 17:30:2組卷：299引用：2難度：0.5 -
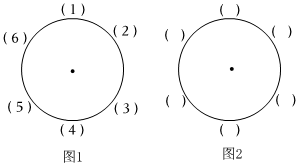2．沿著圓周放著一些數，如果有依次相連的4個數a、b、c、d滿足（a-d）（b-c）＞0，那么就可以交換b、c的位置，這稱為一次操作．
（1）如圖1，圓周上放著數1、2、3、4、5、6，問：能否經過有限次操作后，對圓周上任意依次相連的4個數a、b、c、d,都有（a-d）（b-c）≤0？如果能，請在圖2中填寫出滿足要求的最后結果；如果不能，請說明理由． （2）若圓周上從小到大按順時針依次放著2021個正整數1、2、3、…、2021，問：能否經過有限次操作后，對圓周上任意依次相連的4個數a、b、c、d,都有（a-d）（b-c）≤0？請說明理由．發布：2025/6/4 17:0:1組卷：69引用：1難度：0.3 -
3．法國數學家柯西于1813年在拉格朗日、高斯的基礎上徹底證明了《費馬多邊形數定理》，其主要突破在“五邊形數（點的個數）”的證明上．如圖，這是前幾個“五邊形數”的對應圖形，請據此推斷，第8個“五邊形數”為 ．
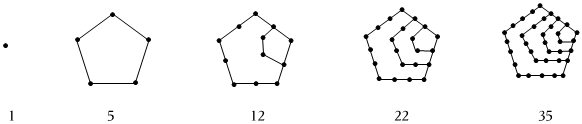發布：2025/6/4 18:30:2組卷：38引用：1難度：0.5