（1）如圖1，在正方形ABCD中，M是BC邊（不含端點B、C）上任意一點，P是BC延長線上一點，N是∠DCP的平分線上一點．若∠AMN=90°，求證：AM=MN．
下面給出一種證明的思路，你可以按這一思路證明，也可以選擇另外的方法證明．
證明：在邊AB上截取AE=MC，連ME．
正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE．
（下面請你完成余下的證明過程）
（2）若將（1）中的“正方形ABCD”改為“正三角形ABC”（如圖2），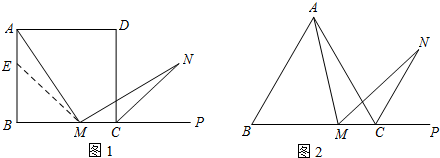
N是∠ACP的平分線上一點，則當∠AMN=60°時，結論AM=MN是否還成立？請說明理由．
【考點】全等三角形的判定與性質；等邊三角形的性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：217引用：5難度：0.5
相似題
-
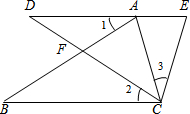1．如圖，已知AC=CE，∠1=∠2=∠3．求證：
（1）∠B=∠D；
（2）AB=ED．發布：2025/5/31 17:30:1組卷：178引用：4難度：0.5 -
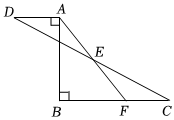2．如圖，已知AB=12，AB⊥BC于點B，AB⊥AD于點A，點E是CD的中點，連接AE并延長交BC于點F，AD=5，BC=10，則AE的長為 ．發布：2025/5/31 16:30:2組卷：815引用：6難度：0.6 -
3．如圖，F、G、H在直線AC上，EF∥BG∥DH，BG⊥AC，AE⊥AB且AE=AB，BC⊥CD且BC=CD．
（1）求證：△FEA≌△GAB；
（2）請按照圖中所標注的數據，計算圖中實線所圍成的圖形的面積．發布：2025/5/31 16:30:2組卷：84引用：1難度：0.5