觀察下列各式的規律：1×3=2²-1；3×5=4²-1；5×7=6²-1；7×9=8²-1…請將發現的規律用含n的式子表示為
（2n-1）（2n+1）=（2n）²-1
（2n-1）（2n+1）=（2n）²-1
．

【答案】（2n-1）（2n+1）=（2n）²-1

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/6/5 9:30:2組卷：110引用：3難度：0.6

相似題

1．已知a₁、a₂、a₃、…、a_n是從1或0中取值的一列數（1和0都至少有一個），若
（
a
1
+
2
）
2
+
（
a
2
+
2
）
2
+
（
a
3
+
2
）
2
+
…
+
（
a
n
+
2
）
2
=
81
，則這列數的個數n為
．
發布：2025/6/6 19:30:1組卷：359引用：4難度：0.4
解析
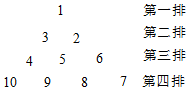2．將正整數按如圖所示的規律排列下去，若有序數對（n,m）表示第n排，從左到右第m個數，如（4，2）表示9，則表示120的有序數對是（　　）
A．（15，1） B．（15，15） C．（16，1） D．（16，16）
發布：2025/6/6 18:0:2組卷：127引用：3難度：0.5
解析
3．為了求1+2+2²+2³+…+2¹⁰⁰的值，可令S=1+2+2²+2³+…+2¹⁰⁰，則2S=2+2²+2³+2⁴+…+2¹⁰¹，因此2S-S=2¹⁰¹-1，所以S=2¹⁰¹-1，即1+2+2²+2³+…+2¹⁰⁰=2¹⁰¹-1，仿照以上方法計算1+3+3²+3³+…+3ⁿ的值是
．
發布：2025/6/6 16:0:1組卷：177引用：1難度：0.5
解析

相關試卷

觀察下列各式的規律：1×3=22-1；3×5=42-1；5×7=62-1；7×9=82-1…請將發現的規律用含n的式子表示為 （2n-1）（2n+1）=（2n）2-1（2n-1）（2n+1）=（2n）2-1．