閱讀下面材料：
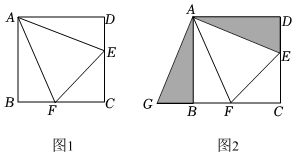
小元遇到這樣一個問題：如圖1，在正方形ABCD中，點E、F分別為DC、BC邊上的點，∠EAF=45°，連結EF，設DE=a,EF=b,FB=c,則把關于x的一元二次方程ax2-bx+c=0叫做正方形ABCD的關聯方程，正方形ABCD叫做方程ax2-bx+c=0的關聯四邊形．
探究方程ax2-bx+c=0是否存在常數根t.
小元是這樣思考的：要想解決這個問題，首先應想辦法把這些分散的線段集中到同一條線段上．他先后嘗試了平移、翻折、旋轉的方法，發現通過旋轉可以解決此問題．他的方法是把△ADE繞點A順時針旋轉90°得到△ABG（如圖2），此時GF即是DE+BF．
請回答：t=11．
參考小元得到的結論和思考問題的方法，解決下列問題：
（1）如圖1，若AD=10，DE=4，則正方形ABCD的關聯方程為 14x2-29x+15=014x2-29x+15=0；
（2）正方形ABCD的關聯方程是2x2-bx+3=0，則正方形ABCD的面積=3636．
【考點】幾何變換綜合題．
【答案】1；14x2-29x+15=0；36
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：575引用：3難度：0.1
相似題
-
1．在△ABC中，AB=AC，點D為BC的中點，點E、F分別在邊AB、AC上，且滿足DE⊥DF．
（1）如圖1，當∠BAC=120°時，若DF∥AB，DE=m,則DF=；
（2）如圖2，當∠BAC=90°時，求證：BE2+CF2=2DE2；
（3）如圖3，當∠BAC=60°時將∠CDF沿DF翻折，CD邊與EF交于點G，若BE=12，CF=20，求EF的長．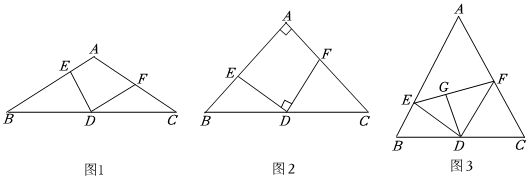
發布：2025/6/10 23:0:2組卷：309引用：3難度：0.2 -
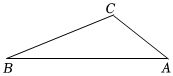2．如圖，△ABC中，∠ACB=120°，將邊AB繞點A逆時針旋轉60°得到線段AD，連接BD，CD．
（1）補全圖形；
（2）猜想DC、BC、AC之間的數量關系，并證明；
（3）若∠BAC=30°，直接寫出DC、AB之間的關系．發布：2025/6/11 1:0:1組卷：29引用：1難度：0.3 -
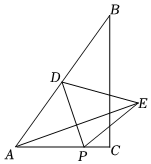3．如圖，在Rt△ABC中，∠C=90°，AC=6，BC=8，動點P從A出發，沿AC以每秒3個單位長度的速度向終點C勻速運動，點D為AB的中點，當點P不與A、C重合時，連結PD，以直線PD為對稱軸作△APD的軸對稱圖形△PED，連結AE，動點P的運動時間為t秒．
（1）線段AB的長為 ．
（2）當直線AE與BC垂直時，求t的值．
（3）當△ADE是鈍角三角形時，求t的取值范圍．發布：2025/6/11 1:30:1組卷：25引用：1難度：0.5