探究題
已知：如圖1，AB∥CD，CD∥EF．
求證：∠B+∠BDF+∠F=360°．
老師要求學生在完成這道教材上的題目證明后，嘗試對圖形進行變式，繼續(xù)做拓展探究，看看有什么新發(fā)現(xiàn)？
（1）小穎首先完成了對這道題的證明，在證明過程中她用到了平行線的一條性質(zhì)，小額用到的平行線性質(zhì)可能是兩直線平行同旁內(nèi)角互補兩直線平行同旁內(nèi)角互補．
（2）接下來，小穎用《幾何畫板》對圖形進行了變式，她先畫了兩條平行線AB、EF，然后在平行線間畫了一點D，連接BD，DF后，用鼠標拖動點D，分別得到了圖①②③，小穎發(fā)現(xiàn)圖②正是上面題目的原型，于是她由上題的結論猜想到圖①和③中的∠B、∠BDF與∠F之間也可能存在著某種數(shù)量關系．于是她利用《幾何畫板》的度量與計算功能，找到了這三個角之間的數(shù)量關系．
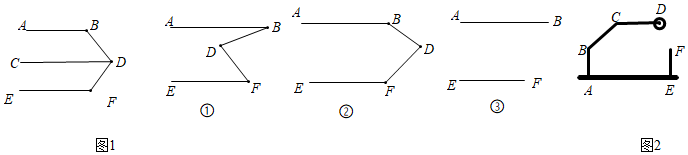
請你在小穎操作探究的基礎上，繼續(xù)完成下面的問題：
①猜想圖①中∠B、∠BDF與∠F之間的數(shù)量關系并加以證明：
②補全圖③，直接寫出∠B、∠BDF與∠F之間的數(shù)量關系：∠F=∠D+∠B∠F=∠D+∠B．
（3）學以致用：一個小區(qū)大門欄桿的平面示意圖如圖2所示，BA垂直地面AE于A，CD平行于地面AE，若∠BCD=150°，則∠ABC=120°120°．
【考點】平行線的判定與性質(zhì)．
【答案】兩直線平行同旁內(nèi)角互補；∠F=∠D+∠B；120°
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：982引用：6難度：0.3
相似題
-
1．【閱讀理解】兩條平行線間的拐點問題經(jīng)常可以通過作一條直線的平行線進行轉(zhuǎn)化．
例如：如圖1，MN∥/PQ，點C、B分別在直線MN、PQ上，點A在直線MN、PO之間．
（1）求證：∠CAB=∠MCA+∠PBA；
證明：如圖1，過點A作AD∥MN．
∵MN∥PQ，AD∥MN，
∴AD∥/MN∥PQ
∴∠MCA=LDAC，∠PBA=∠DAB，
∴∠CAB=∠DAC+∠DAB=∠MCA+∠PBA，
即：∠CAB=∠MCA+∠PBA．
【類比應用】已知直線AB∥CD，P為平面內(nèi)一點，連接PA、PD．
（1）如圖2，已知∠A=50°，∠D=150°，求∠APD的度數(shù)，請說明理由．
（2）如圖3，設∠PAB=α、∠CDP=β，猜想∠α、β、∠P之間的數(shù)量關系為 ．
【聯(lián)系拓展】
（3）如圖4，直線AB∥CD，P為平面內(nèi)一點，連接PA、PD．AP⊥PD，DN平分∠PDC，若∠PAN+∠PAB=∠P，運用（2）中的結論，直接寫出么∠N的度數(shù)，則∠N的度數(shù)為 ．12發(fā)布：2025/5/31 12:0:1組卷：1473引用：2難度：0.4 -
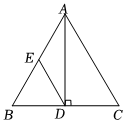2．如圖，已知AB=AC，AD⊥BC于D，DE=AE．
（1）求證：DE∥AC；
（2）若∠C=60°，AC=6，求AD的長．發(fā)布：2025/5/31 12:30:1組卷：251引用：3難度：0.7 -
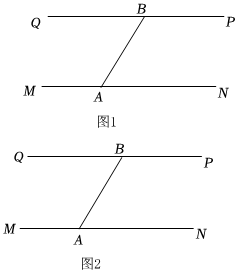3．“成綿樂高鐵”為了安全起見在某段鐵路兩旁安置了兩座可旋轉(zhuǎn)探照燈．如圖1所示燈A射線從AM開始順時針旋轉(zhuǎn)至AN便立即回轉(zhuǎn)，燈B射線從BP開始順時針旋轉(zhuǎn)至BQ便立即回轉(zhuǎn)，兩燈不停交叉照射巡視．若燈A轉(zhuǎn)動的速度是每秒3度，燈B轉(zhuǎn)動的速度是每秒2度，假定主道路是平行的，即PQ∥MN，且∠BAM：∠BAN=2：1．
（1）填空：∠BAN=；
（2）若燈B射線先轉(zhuǎn)動15秒，燈A射線才開始轉(zhuǎn)動，在燈B射線到達BQ之前，A燈轉(zhuǎn)動幾秒，兩燈的光束互相平行？
（3）如圖2，若兩燈同時開始轉(zhuǎn)動，兩燈射出的光束交于點C，則在燈B射線到達BQ之前，A燈轉(zhuǎn)動幾秒時，∠ACB=120°．發(fā)布：2025/5/31 12:30:1組卷：810引用：1難度：0.1