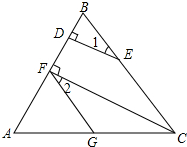
如圖，已知CF⊥AB于F，ED⊥AB于D，∠1=∠2，求證：FG∥BC．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/6/8 15:0:1組卷：3115引用：33難度：0.5

相似題

1．已知的三角形的三個內角的度數和是180°，如圖是兩個三角板不同位置的擺放，其中∠ACB=∠CDE=90°，∠BAC=60°，∠DEC=45°．

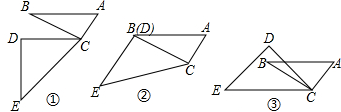
（1）當AB∥DC時，如圖①，求∠DCB的度數．
（2）當CD與CB重合時，如圖②，判斷DE與AC的位置關系，并說明理由．
（3）如圖③，當∠DCB等于
度時，AB∥EC．
發布：2025/6/8 19:0:1組卷：172引用：4難度：0.5
解析
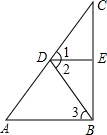2．如圖，∠1=∠2，DE⊥BC，AB⊥BC，那么∠A=∠3嗎？說明理由．
解：∠A=∠3，理由如下：
∵DE⊥BC，AB⊥BC（已知）
∴∠DEB=∠ABC=90°（
）
∴∠DEB+（
）=180°
∴DE∥AB（
）
∴∠1=∠A（
）
∠2=∠3（
）
∵∠1=∠2（已知）
∴∠A=∠3（
）
發布：2025/6/8 19:0:1組卷：304引用：9難度：0.5
解析
3．將一副三角板按如圖放置，則下列結論：
①∠1=∠3；②如果∠2=30°，則有AC∥DE；③∠2+∠CAD=180°；④如果∠4=∠C，必有AB⊥ED．其中正確的有
（填寫序號）
發布：2025/6/8 19:0:1組卷：354引用：6難度：0.7
解析

相關試卷

2．如圖，∠1=∠2，DE⊥BC，AB⊥BC，那么∠A=∠3嗎？說明理由．解：∠A=∠3，理由如下：∵DE⊥BC，AB⊥BC（已知）∴∠DEB=∠ABC=90°（）∴∠DEB+（）=180°∴DE∥AB（）∴∠1=∠A（）∠2=∠3（）∵∠1=∠2（已知）∴∠A=∠3（）