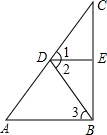
如圖，∠1=∠2，DE⊥BC，AB⊥BC，那么∠A=∠3嗎？說明理由．
解：∠A=∠3，理由如下：
∵DE⊥BC，AB⊥BC（已知）
∴∠DEB=∠ABC=90°（垂直的定義垂直的定義）
∴∠DEB+（∠ABC∠ABC）=180°
∴DE∥AB（同旁內角互補，兩直線平行同旁內角互補，兩直線平行）
∴∠1=∠A（兩直線平行，同位角相等兩直線平行，同位角相等）
∠2=∠3（兩直線平行，內錯角相等兩直線平行，內錯角相等）
∵∠1=∠2（已知）
∴∠A=∠3（等量代換等量代換）
【考點】平行線的判定與性質．
【答案】垂直的定義；∠ABC；同旁內角互補，兩直線平行；兩直線平行，同位角相等；兩直線平行，內錯角相等；等量代換
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/8 19:0:1組卷：304引用：9難度：0.5
相似題
-
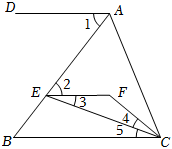1．已知：∠DAC+∠ACB=180°，∠1=∠2，∠3=∠4，CE平分∠BCF嗎？請說明理由．發布：2025/6/9 1:0:1組卷：450引用：1難度：0.5 -
2．完成下面的填空．
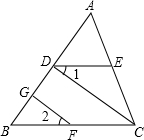
如圖，已知FG⊥AB，CD⊥AB，垂足分別為G，D，∠1=∠2．
證明：∠CED+∠ACB=180°
請你將小明的證明過程補充完整．
證明：∵FG⊥AB，CD⊥AB，垂足分別為G，D（已知），
∴∠FGB=∠CDB=90° （ ）．
∴GF∥CD（ ）．
∵GF∥CD（已證），
∴∠2=∠BCD （ ）．
又∵∠1=∠2（已知），
∴∠1=∠BCD （ ）．
∴DE∥BC （ ）．
∴∠CED+∠ACB=180° （ ）．發布：2025/6/9 2:30:1組卷：221引用：3難度：0.7 -
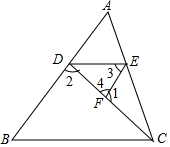3．如圖所示，已知∠1+∠2=180°，∠B=∠3，求證：∠ACB=∠AED．發布：2025/6/9 0:0:2組卷：999引用：14難度：0.3