【操作發(fā)現(xiàn)】（1）如圖1是一個(gè)長為4b、寬為a的長方形，沿圖1中虛線用剪刀平均分成四塊小長方形，然后用四塊小長方形拼成的一個(gè)“回形”正方形（如圖2），那么圖2中的陰影部分的面積為：（a-b）2（a-b）2（用a,b的代數(shù)式表示）；觀察圖2，請(qǐng)你寫出 （a+b）2，（a-b）2，ab之間的等量關(guān)系是 （a+b）2=（a-b）2+4ab（a+b）2=（a-b）2+4ab．
【靈活應(yīng)用】（2）運(yùn)用你所得到的公式計(jì)算：若x,y為實(shí)數(shù)，且x-y=7，xy=154，求x+y的值；
【拓展遷移】（3）將兩塊全等的特制直角三角板△AOB，△COD （∠AOB=∠COD=90°按如圖3所示的方式放置，A，O，D在同一直線上，連接AC，BD．若AD=14，S△AOC+S△BOD=50，求陰影部分的面積．
xy
=
15
4
【考點(diǎn)】完全平方公式的幾何背景；全等三角形的性質(zhì)．
【答案】（a-b）2；（a+b）2=（a-b）2+4ab
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/9 8:0:9組卷：1218引用：6難度：0.6
相似題
-
1．若x滿足（9-x）（x-4）=4，求（4-x）2+（x-9）2的值．
解：設(shè)9-x=a,x-4=b,則（9-x）（x-4）=ab=4，a+b=（9-x）+（x-4）=5，
∴（9-x）2+（x-4）2=（a+b）2-2ab=52-2×4=17．
請(qǐng)仿照上面的方法求解下面問題：
（1）若x滿足（5-x）（x-2）=2，求（5-x）2+（x-2）2的值．
（2）若x滿足（6-x）（3-x）=1，求代數(shù)式（9-2x）2的值．
（3）已知正方形ABCD的邊長為x,E，F(xiàn)分別是AD、DC上的點(diǎn)，且AE=3，CF=5，長方形EMFD的面積是48，分別以MF、DF作正方形，求陰影部分的面積．發(fā)布：2025/6/2 13:0:2組卷：642引用：2難度：0.7 -
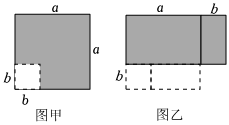2．如圖，在邊長為a的正方形中挖去一個(gè)邊長為b的|小正方形（a＞b）（如圖甲），把余下的部分拼成一個(gè)矩形（如圖乙），根據(jù)兩個(gè)圖形中陰影部分的面積相等，可以驗(yàn)證的等式是 ．發(fā)布：2025/6/2 13:0:2組卷：242引用：2難度：0.6 -
3．如圖a是一個(gè)長為2m、寬為2n的長方形，沿圖中虛線用剪刀均勻分成四塊小長方形，然后按圖b形狀拼成一個(gè)正方形．
（1）你認(rèn)為圖b中的陰影部分的正方形的邊長等于多少？
（2）觀察圖b你能寫出下列三個(gè)代數(shù)式之間的等量關(guān)系嗎？
代數(shù)式：（m+n）2，（m-n）2，mn
（3）已知m+n=7，mn=6，求（m-n）2的值．發(fā)布：2025/6/2 11:30:1組卷：2828引用：12難度：0.3