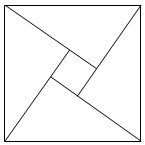
 “趙爽弦圖”是四個全等的直角三角形與中間一個小正方形拼成的大正方形,如圖,每一個直角三角形的兩條直角的長分別是3和4,則中間的小正方形和大正方形的面積比是( )
“趙爽弦圖”是四個全等的直角三角形與中間一個小正方形拼成的大正方形,如圖,每一個直角三角形的兩條直角的長分別是3和4,則中間的小正方形和大正方形的面積比是( )
【答案】B
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/5/27 14:0:0組卷:69引用:2難度:0.5
相似題
-
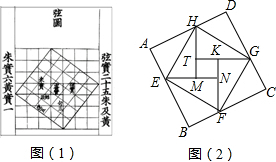 1.勾股定理被譽為“幾何明珠”,在數學的發展歷程中占有舉足輕重的地位.中國數學史上最先完成勾股定理證明的數學家是公元3世紀三國時期的趙爽,他為了證明勾股定理,創制了一幅“弦圖”,后人稱其為“趙爽弦圖”(如圖(1)所示).圖(2)由弦圖變化得到,它是由八個全等的直角三角形拼接而成的.記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3,若S1+S2+S3=129,則S2的值是 .發布:2025/6/13 12:30:10組卷:109引用:4難度:0.6
1.勾股定理被譽為“幾何明珠”,在數學的發展歷程中占有舉足輕重的地位.中國數學史上最先完成勾股定理證明的數學家是公元3世紀三國時期的趙爽,他為了證明勾股定理,創制了一幅“弦圖”,后人稱其為“趙爽弦圖”(如圖(1)所示).圖(2)由弦圖變化得到,它是由八個全等的直角三角形拼接而成的.記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3,若S1+S2+S3=129,則S2的值是 .發布:2025/6/13 12:30:10組卷:109引用:4難度:0.6 -
2.勾股定理是歷史上第一個把數與形聯系起來的定理,其證明是論證幾何的發端.下面四幅圖中不能證明勾股定理的是( )
A. 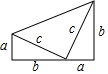
B. 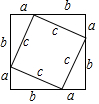
C. 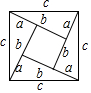
D. 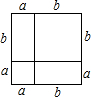 發布:2025/6/13 13:30:1組卷:2251引用:21難度:0.8
發布:2025/6/13 13:30:1組卷:2251引用:21難度:0.8 -
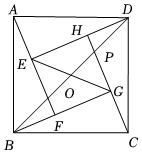 3.如圖,四個全等的直角三角形拼成“趙爽弦圖”,得到正方形ABCD與正方形EFGH.連結EG,BD相交于點O、BD與HC相交于點P.若GO=GP,則的值是( )S△ABDS△EFG
3.如圖,四個全等的直角三角形拼成“趙爽弦圖”,得到正方形ABCD與正方形EFGH.連結EG,BD相交于點O、BD與HC相交于點P.若GO=GP,則的值是( )S△ABDS△EFGA.1+ 2B.2+ 2C.5- 2D. 154發布:2025/6/13 14:0:2組卷:2136引用:5難度:0.3


