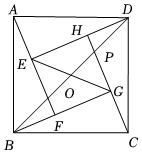
如圖，四個全等的直角三角形拼成“趙爽弦圖”，得到正方形ABCD與正方形EFGH．連結EG，BD相交于點O、BD與HC相交于點P．若GO=GP，則S△ABDS△EFG的值是（ ）
S
△
ABD
S
△
EFG
【考點】勾股定理的證明．
【答案】B
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/13 14:0:2組卷：2136引用：5難度：0.3
相似題
-
1．如圖是“趙爽弦圖”，△ABH、△BCG、△CDF和△DAE是四個全等的直角三角形，四邊形ABCD和EFGH是正方形，如果AH=6，EF=2，那么AB=．發布：2025/6/15 2:30:1組卷：103引用：2難度：0.7 -
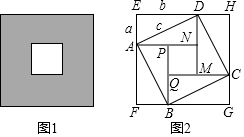2．小穎用四塊完全一樣的長方形方磚，恰好拼成如圖1所示圖案，如圖2，連接對角線后，她發現該圖案中可以用“面積法”采用不同方案去證明勾股定理．設AE=a,DE=b,AD=c,請你找到其中一種方案證明：a2+b2=c2．發布：2025/6/15 2:30:1組卷：617引用：2難度：0.5 -
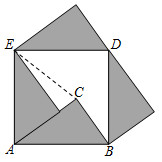3．清代數學家梅文鼎在《勾股舉隅》一書中，用四個全等的直角三角形拼出正方形ABDE的方法證明了勾股定理（如圖），若Rt△ABC的斜邊AB=5，BC=3，則圖中線段CE的長為．發布：2025/6/14 21:30:2組卷：1094引用：14難度：0.7