某公司購進(jìn)某種水果的成本為20元/千克,經(jīng)過市場調(diào)研發(fā)現(xiàn),這種水果在未來48天的銷售價格p(元/千克)與時間t(天)之間的函數(shù)關(guān)系式為
p=14t+30(1≤t≤24,t為整數(shù)) -12t+48(25≤t≤48,t為整數(shù))
,且其日銷售量y(千克)與時間t(天)的關(guān)系如下表:
1 4 t + 30 ( 1 ≤ t ≤ 24 , t 為整數(shù) ) |
- 1 2 t + 48 ( 25 ≤ t ≤ 48 , t 為整數(shù) ) |
| 時間t/天 | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日銷售量y/千克 | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)問哪一天的銷售利潤最大?最大日銷售利潤為多少?
(3)在實(shí)際銷售的前24天中,公司決定每銷售1千克水果就捐贈n元利潤(n<9)給“精準(zhǔn)扶貧”對象.現(xiàn)發(fā)現(xiàn):在前24天中,每天扣除捐贈后的日銷售利潤隨時間t的增大而增大,求n的取值范圍.
【考點(diǎn)】二次函數(shù)的應(yīng)用.
【答案】見試題解答內(nèi)容
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:391引用:4難度:0.3
相似題
-
1.用各種盛水容器可以制作精致的家用流水景觀(如圖1).
科學(xué)原理:如圖2,始終盛滿水的圓柱體水桶水面離地面的高度為H(單位:cm),如果在離水面豎直距離為h(單位:cm)的地方開大小合適的小孔,那么從小孔射出水的射程(水流落地點(diǎn)離小孔的水平距離)s(單位:cm)與h的關(guān)系式為s2=4h(H-h).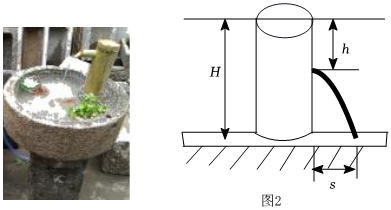
應(yīng)用思考:現(xiàn)用高度為30cm的圓柱體塑料水瓶做相關(guān)研究,水瓶直立地面,通過連續(xù)注水保證它始終盛滿水,在離水面豎直距離h cm處開一個小孔.
(1)寫出s2與h的關(guān)系式;并求出當(dāng)h為何值時,射程s有最大值,最大射程是多少?
(2)在側(cè)面開兩個小孔,這兩個小孔離水面的豎直距離分別為a,b,要使兩孔射出水的射程相同,求a,b之間的關(guān)系式;
(3)如果想通過墊高塑料水瓶,使射出水的最大射程增加18cm,求墊高的高度及小孔離水面的豎直距離.發(fā)布:2025/6/11 8:0:2組卷:251引用:3難度:0.4 -
,所以x-2
2.知識背景:
當(dāng)a>0且x>0時,因?yàn)?div dealflag="1" class="MathJye" mathtag="math">(x-ax)2≥0≥0,a+ax
從而(當(dāng)x+ax≥2a=x,即x=ax時取等號).a
設(shè)函數(shù)y=x+(x>0,a>0),由上述結(jié)論可知:當(dāng)x=ax時,該函數(shù)有最小值2a.a
應(yīng)用舉例
已知函數(shù)為y1=x(x>0)與函數(shù)y2=(x>0),則當(dāng)x=3x時,y1+y2=x+3有最小值為23x.3
解決問題
(1)已知函數(shù)為y1=x-1(x>1)與函數(shù)y2=(x-1)2+9(x>1),當(dāng)x取何值時,有最小值?最小值是多少?y2y1
(2)已知某設(shè)備租賃使用成本包含以下三部分:一是設(shè)備的安裝調(diào)試費(fèi)用,共490元;二是設(shè)備的租賃使用費(fèi)用,每天200元;三是設(shè)備的折舊費(fèi)用,它與使用天數(shù)的平方成正比,比例系數(shù)為0.001.若設(shè)該設(shè)備的租賃使用天數(shù)為x天,則當(dāng)x取何值時,該設(shè)備平均每天的租賃使用成本最低?最低是多少元?
發(fā)布:2025/6/11 6:30:1組卷:218引用:2難度:0.5
3.根據(jù)物理學(xué)規(guī)律,如果不考慮空氣阻力,以40m/s的速度將小球沿與地面成30°角的方向擊出,小球的飛行高度h(單位:m)與飛行時間t(單位:s)之間的函數(shù)關(guān)系是h=-5t2+20t,當(dāng)飛行時間t為 s時,小球達(dá)到最高點(diǎn).
發(fā)布:2025/6/11 6:0:1組卷:2964引用:42難度:0.9


