【探究發(fā)現(xiàn)】
按圖中方式將大小不同的兩個正方形放在一起，分別求出陰影部分（△ACF）的面積．
（單位：厘米，陰影部分的面積依次用S1、S2、S3表示） 
（1）S1=5050cm2； S2=5050cm2； S3=5050cm2．
（2）上題中，重新設(shè)定正方形ABCD的邊長，AB=2020cm,并再次分別求出陰影部分（△ACF）的面積：
S1=200200cm2； S2=200200cm2； S3=200200cm2．
（3）歸納總結(jié)你的發(fā)現(xiàn)：S△ACF=12S正方形ABCD．S△ACF=12S正方形ABCD．
【推理反思】
按（圖甲）中方式將大小不同的兩個正方形放在一起，設(shè)小正方形的邊長是bcm,大正方形的邊長是a cm,求：陰影部分（△ACF）的面積．
【應(yīng)用拓展】
（1）按（圖甲）方式將大小不同的兩個正方形放在一起，若大正方形的面積是80cm2，則圖甲中陰影三角形的面積是4040cm2．
（2）如圖乙，C是線段AB上任意一點，分別以AC、BC為邊在線段AB同側(cè)構(gòu)造等邊三角形△ACD和等邊三角形△CBE，若△CBE的面積是1cm2，則圖乙中陰影三角形的面積是11 cm2．
1
2
1
2
【考點】四邊形綜合題．
【答案】50；50；50；20；200；200；200；S△ACF=S正方形ABCD．；40；1
1
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：272引用：2難度：0.5
相似題
-
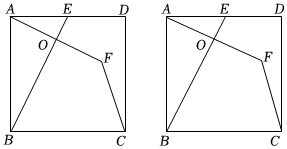1．如圖，正方形ABCD中，點E在邊AD上（不與端點A，D重合），點A關(guān)于直線BE的對稱點為點F，連接CF，設(shè)∠ABE=α．
（1）求∠AFC的大小；
（2）過點C作CG⊥AF，垂足為G，連接DG．
①求證：DG∥CF；
②連接OD，若OD⊥DG，求sinα的值．發(fā)布：2025/5/31 13:30:2組卷：1339引用：5難度：0.3 -
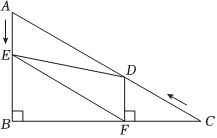2．如圖，在Rt△ABC中，∠B=90°，AC=10，∠C=30°，點D從點C出發(fā)沿CA方向以每秒2個單位長度的速度向點A勻速運動，同時點E從點A出發(fā)沿AB方向以每秒1個單位長度的速度向點B勻速運動，當(dāng)其中一個點到達(dá)終點時，另一個點也隨之停止運動．設(shè)點D、E運動的時間是t（t＞0）秒，過點D作DF⊥BC于點F，連接DE、EF．
（1）求證：四邊形AEFD是平行四邊形；
（2）當(dāng)t為何值時，△DEF是等邊三角形？說明理由；
（3）當(dāng)t為何值時，△DEF為直角三角形？（請直接寫出t的值）發(fā)布：2025/5/31 17:0:8組卷：981引用：4難度：0.1 -
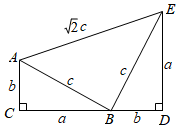3．如圖，四邊形ACDE是證明勾股定理時用到的一個圖形，a,b,c是Rt△ABC和Rt△BED邊長，易知AE=c,這時我們把關(guān)于x的形如ax2+2cx+b=0的一元二次方程稱為“勾系一元二次方程”．2
請解決下列問題：
（1）判斷下列方程是否是“勾系一元二次方程”：
①2x2+x+1=0 （填“是”或“不是”）；5
②3x2+5x+4=0 （填“是”或“不是”）2
（2）求證：關(guān)于x的“勾系一元二次方程”ax2+cx+b=0必有實數(shù)根；2
（3）若x=-1是“勾系一元二次方程”ax2+cx+b=0的一個根，且四邊形ACDE的周長是12，求△ABC面積．2發(fā)布：2025/5/31 14:0:2組卷：623引用：4難度：0.3