綜合與實踐
【背景介紹】
勾股定理是幾何學中的明珠，充滿著魅力．勾股定理是用代數思想解決幾何問題的最重要的工具之一，它不但因證明方法層出不窮吸引著人們，更因為應用廣泛而使人著迷．
【證明方法】
如圖1是著名的趙爽弦圖，由四個全等的直角三角形拼成，用它可以證明勾股定理，思路是大正方形的面積有兩種求法，一種是等于c2，另一種是等于四個直角三角形與一個小正方形的面積之和，即12ab×4+（b-a）2，從而得到等式c2=12ab×4+（b-a）2，化簡便得結論．a2+b2=c2．這里用兩種求法來表示同一個量從而得到等式或方程的方法，我們稱之為“雙求法”．
【方法應用】
請利用“雙求法”解決下面的問題：
（1）如圖2，小正方形邊長為1，連接小正方形的三個頂點，可得△ABC，則AB邊上的高為 141717141717．
【方法遷移】
（2）如圖3，在△ABC中，AC=14，AB=16，BC=6，AD是BC邊上的高，求AD的值．
【定理應用】
（3）如圖4，在長方形ABCD中，AB=3，AB在數軸上，若以點A為圓心，對角線AC的長為半徑作弧交數軸的正半軸于點M，則點M表示的數為 13-213-2．
【數學思想】
（4）在解決以上問題的過程中，讓我們感悟的數學思想有 ①②①②（填序號）．
①方程思想
②數形結合思想
③分類討論思想
④函數思想
1
2
ab
×
4
+
（
b
-
a
）
2
c
2
=
1
2
ab
×
4
+
（
b
-
a
）
2
14
17
17
14
17
17
13
13
【答案】；-2；①②
14
17
17
13
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/28 17:0:1組卷：196引用：3難度：0.5
相似題
-
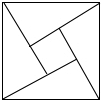1．“趙爽弦圖”巧妙地利用面積關系證明了勾股定理，是我國古代數學的驕傲，如圖所示的“趙爽弦圖”是由四個全等的直角三角形和一個小正方形拼成的一個大正方形．設直角三角形較長直角邊長為a,較短直角邊長為b,若ab=8，大正方形的面積為25，則小正方形的邊長為．發布：2025/6/20 3:0:1組卷：3792引用：52難度：0.6 -
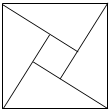2．如圖，“趙爽弦圖”是由四個全等的直角三角形與一個小正方形拼成大正方形，若小正方形的邊長為3，大正方形邊長為15，則一個直角三角形的周長是（ ）發布：2025/6/20 8:30:2組卷：1183引用：9難度：0.5 -
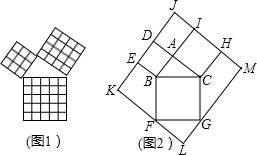3．勾股定理是幾何中的一個重要定理．在我國古算書《周髀算經》中就有“若勾三，股四，則弦五”的記載．如圖1是由邊長相等的小正方形和直角三角形構成的，可以用其面積關系驗證勾股定理．圖2是由圖1放入矩形內得到的，∠BAC=90°，AB=3，AC=4，點D，E，F，G，H，I都在矩形KLMJ的邊上，則矩形KLMJ的面積為（ ）發布：2025/6/19 1:30:1組卷：7215引用：73難度：0.9