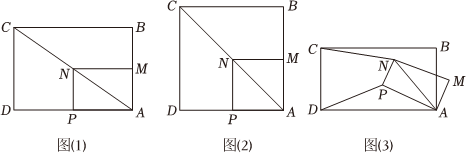
如圖(1),在矩形ABCD中,AD=nAB,點M,P分別在邊AB,AD上(均不與端點重合),且AP=nAM,以AP和AM為鄰邊作矩形AMNP,連接AN,CN.
【問題發(fā)現(xiàn)】
(1)如圖(2),當n=1時,BM與PD的數(shù)量關系為 BM=PDBM=PD,CN與PD的數(shù)量關系為 CN=2PDCN=2PD.
【類比探究】
(2)如圖(3),當n=2時,矩形AMNP繞點A順時針旋轉(zhuǎn),連接PD,則CN與PD之間的數(shù)量關系是否發(fā)生變化?若不變,請就圖(3)給出證明;若變化,請寫出數(shù)量關系,并就圖(3)說明理由.
【拓展延伸】
(3)在(2)的條件下,已知AD=4,AP=2,當矩形AMNP旋轉(zhuǎn)至C,N,M三點共線時,請寫出線段CN的長并說明理由.
2
2
【考點】四邊形綜合題.
【答案】BM=PD;CN=PD
2
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/9/7 1:0:8組卷:443引用:9難度:0.2
相似題
-
1.【閱讀與思考】平移是初中幾何變換之一,它可以將線段和角平移到一個新的位置,從而把分散的條件集中到一起,使問題得以解決.
【問題情景】如圖1,在正方形中ABCD中,E、F、G分別是BC、CD、AD上的點,GE⊥BF于點O,求證:GE=BF.
小明嘗試平移線段GE到AH,構(gòu)造△ABH≌△BCF,使問題得到解決.
(1)【閱讀理解】按照小明的思路,證明△ABH≌△BCF的依據(jù)是 ;
(2)【嘗試應用】
如圖2,在5×6的正方形網(wǎng)格中,點A、B、C、D為格點,AB交CD于點M.則∠AMC的度數(shù)為 ;
(3)如圖3,在正方形方格紙中,每個小正方形的邊長都相等,A、B、C、D都在格點處,AB與CD相交于點P,求tan∠APC的值.發(fā)布:2025/5/21 23:0:1組卷:403引用:5難度:0.1 -
2.如圖①~⑧是課本上的折紙活動.

【重溫舊知】
上述活動,有的是為了折出特殊圖形,如圖①、③和⑧;有的是為了發(fā)現(xiàn)或證明定理,如圖④和⑦;有的是計算角度,如圖②;有的是計算長度,如圖⑤和⑥.
(1)圖③中的△ABC的形狀是 ,圖④的活動發(fā)現(xiàn)了定理“”(注:填寫定理完整的表述),圖⑤中的BF的長是 .
【新的發(fā)現(xiàn)】
(2)圖⑧中,在第3次折后,點D落在點D′處,直接寫出點D'的位置特點.
【換種折法】
(3)圖⑧中,在第1次折后,再次折疊,如圖⑨,使點A與點F重合,折痕為MN,點D落在點D″處,F(xiàn)D″與CD交于點P.說明P為CD的三等分點.
【繼續(xù)探索】
(4)如何折疊正方形紙片ABCD得到邊AD的五等分點?請畫出示意圖,簡述折疊過程,并說明理由.發(fā)布:2025/5/21 23:0:1組卷:656引用:2難度:0.3 -
3.如圖,正方形ABCD的頂點B在矩形AEFG的邊EF上運動.

(1)如圖1,點C在FG上,求∠FBG的大小;
(2)如圖1,若C是FG的中點,求證:CH=DH;
(3)如圖2,若AE=2,EF=3,設EB=x,CG2=y,直接寫出y與x的函數(shù)解析式(不需要寫自變量的取值范圍).發(fā)布:2025/5/21 22:30:1組卷:246引用:1難度:0.2


