小明在探究三角形與圓的位置變化關系時，發現圖形隨著圓的位置變化存在一些特殊的關系．探究過程如下：如圖，已知在等腰△ABC中，AC=BC，已知AB=6，sin∠OAD=45，點O是AB邊上一點，以OA為半徑作⊙O，發現：⊙O始終與邊AB，邊AC相交，與邊AC的交點記為點D．連結OD，作點C關于直線OD的對稱點C′，連結AC′、DC′、CC′．小明按照以下步驟進行探究：
（1）直接寫出AC的長：55．
（2）設OA=x,DC=y.
①求y關于x的函數表達式．
②當CC'=165 時，求x的值．
（3）點O在邊AB上移動，當△AC′D是以DC′為腰的等腰三角形時，求OA的長．
4
5
16
5
【考點】圓的綜合題．
【答案】5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/2 8:0:9組卷：167引用：4難度：0.4
相似題
-
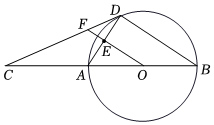1．如圖，AB為⊙O的直徑，點C在BA延長線上，點D在⊙O上，連接CD，AD，∠ADC=∠B，OF⊥AD于點E，交CD于點F．
（1）求證：CD是⊙O的切線；
（2）若S△COF：S△CBD=9：16，求sinC的值．發布：2025/5/23 18:30:2組卷：300引用：1難度：0.4 -
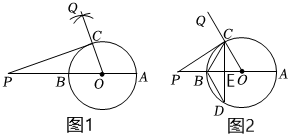2．如圖1，小明在⊙O外取一點P，作直線PO分別交⊙O于B，A兩點，先以點P為圓心，PO的長為半徑畫弧，再以點O為圓心，AB的長為半徑畫弧，兩弧交于點Q，連接OQ，交⊙O于點C，連接PC．完成下列任務：
（1）小明得出PC為⊙O的切線的依據是 ；
（2）如圖2，繼續作點C關于直線AB的對稱點D，連接CD，交AB于點E，連接BD．
①求證：∠PCD=2∠BDC；
②若⊙O的半徑為15，BE=6，求PC的長．發布：2025/5/23 20:0:1組卷：348引用：3難度：0.3 -
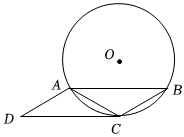3．如圖，⊙O是△ABC的外接圓，分別過A，C作AD∥BC，CD∥AB．
（1）求證：AD=BC；
（2）若AC=BC．
①求證：CD是⊙O的切線；
②已知AB=6cm,當四邊形ABCD的某條邊所在直線過圓心O時，求⊙O的半徑．發布：2025/5/23 17:30:1組卷：150引用：2難度：0.1