（1）問題發現：如圖①，直線AB∥CD，連結BE，CE，可以發現∠BEC=∠B+∠C．
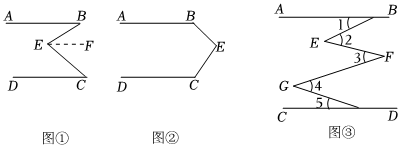
請把下面的證明過程補充完整：
證明：過點E作EF∥AB，
∴∠B=∠BEF（ 兩直線平行，內錯角相等兩直線平行，內錯角相等）．
∵AB∥DC（已知），EF∥AB，
∴EF∥DC（ 平行于同一直線的兩直線平行平行于同一直線的兩直線平行）．
∴∠C=∠CEF．
∵（ ∠B+∠C∠B+∠C）=∠BEF+∠CEF，
∴∠BEC=∠B+∠C．（等量代換）．
（2）拓展探究：如果點E運動到圖②所示的位置，其他條件不變，說明：∠B+∠C=360°-∠BEC．
（3）解決問題：如圖③，AB∥DC，E、F、G是AB與CD之間的點，直接寫出∠1，∠2，∠3，∠4，∠5之間的數量關系．
【考點】平行線的判定與性質．
【答案】兩直線平行，內錯角相等；平行于同一直線的兩直線平行；∠B+∠C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/1 15:30:1組卷：1295引用：2難度：0.6
相似題
-
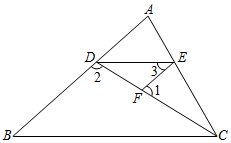1．如圖，已知∠1+∠2=180°，∠3=∠B．
（1）試判斷DE與BC的位置關系，并說明理由．
（2）若DE平分∠ADC，∠2=3∠B，求∠1的度數．發布：2025/6/3 10:0:1組卷：3999引用：24難度：0.6 -
2．【閱讀理解】：兩條平行線間的拐點問題經常可以通過作一條直線的平行線進行轉化．例如：如圖1，MN∥PQ，點C、B分別在直線MN、PQ上，點A在直線MN、PQ之間．
求證：∠CAB=∠MCA+∠PBA；
證明：如圖1，過點A作AD∥MN，
∵MN∥PQ，AD∥MN，
∴AD∥MN∥PQ，
∴∠MCA=∠DAC，∠PBA=∠DAB，
∴∠CAB=∠DAC+∠DAB=∠MCA+∠PBA，
即：∠CAB=∠MCA+∠PBA；
【類比應用】已知直線AB∥CD，P為平面內一點，連接PA、PD．
（1）如圖2，已知∠A=50°，∠D=150°，求∠APD的度數，說明理由；
（2）如圖3，設∠PAB=α、∠CDP=β、直接寫出α、β、∠P之間的數量關系為 ．
【聯系拓展】如圖4，直線AB∥CD，P為平面內一點，連接PA、PD．AP⊥PD，DN平分∠PDC，若∠PAN+∠PAB=∠P，運用（2）中的結論，求∠N的度數，說明理由．12
發布：2025/6/3 8:30:1組卷：1110引用：8難度：0.4 -
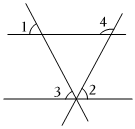3．如圖，已知∠1=∠2=∠3=63°，∠4=．發布：2025/6/3 4:30:1組卷：24引用：2難度：0.7