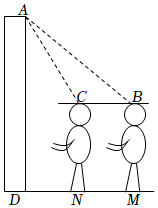
如圖為某學校門口“測溫箱”截面示意圖，當身高1.7米的小聰在地面M處時開始顯示額頭溫度，此時在額頭B處測得A的仰角為45°，當他在地面N處時，此時在額頭C處測得A的仰角為58°，如果測溫箱頂部A處距地面的高度AD為3.3米，求B、C兩點的距離．（結果保留一位小數，sin58°≈0.8，cos58°≈0.5，tan58°≈1.6）
【考點】解直角三角形的應用-仰角俯角問題．
【答案】約為0.6米．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/26 0:30:1組卷：632引用：7難度：0.5
相似題
-
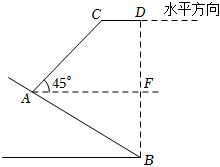1．如圖，一架無人機在滑雪賽道的一段坡道AB的上方進行跟蹤拍攝，無人機伴隨運動員水平向右飛行．某次拍攝中，當運動員在點A位置時，無人機在他的仰角為45°的斜上方C處，當運動員到達地面B點時，無人機恰好到達運動員正上方的D處，已知AB的坡度為1：且長為300米，無人機飛行距離CD為60米，求無人機離地面的高度BD的長．（參考數據：3≈1.7）3發布：2025/5/26 7:30:2組卷：272引用：2難度：0.5 -
2．如圖，某編輯部辦公樓（矩形ABCD）前有一建筑物（矩形MGHN），建筑物垂直于地面，在辦公樓底A處測得建筑物頂的仰角為37°，在辦公樓天臺B處測得建筑物的俯角為45°，已知辦公樓高度AB為14m,求建筑物的高度MN．（參考數據sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）發布：2025/5/26 8:0:5組卷：972引用：5難度：0.5 -
3．如圖是某機場監控屏顯示兩飛機的飛行圖象，1號指揮機（看成點P）始終以3km/min的速度在離地面5km高的上空勻速向右飛行，2號試飛機（看成點Q）一直保持在1號機P的正下方．2號機從原點O處沿45°仰角爬升，到4km高的A處便立刻轉為水平飛行，再過1min到達B處開始沿直線BC降落，要求1min后到達C（10，3）處．
（1）求OA的h關于s的函數解析式，并直接寫出2號機的爬升速度；
（2）求BC的h關于s的函數解析式，并預計2號機著陸點的坐標；
（3）通過計算說明兩機距離PQ不超過3km的時長是多少．
[注：（1）及（2）中不必寫s的取值范圍]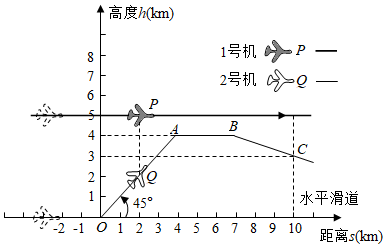
發布：2025/5/26 7:0:2組卷：2355引用：8難度：0.5