閱讀以下材料,并按要求完成相應(yīng)的任務(wù).
定義:自一點(diǎn)引出的兩條射線分別經(jīng)過已知線段的兩端,則這兩條射線所成的角稱為該點(diǎn)對(duì)已知線段的視角.如圖(1),∠APB是點(diǎn)P對(duì)線段AB的視角. 問題:已知在足球比賽中,足球?qū)η蜷T的視角越大,球越容易被踢進(jìn),如圖(2),EF是球門,球員沿直線/帶球前進(jìn),那么他應(yīng)當(dāng)在哪個(gè)地方射門,才能使進(jìn)球的可能性最大? 愛好足球運(yùn)動(dòng)的小明進(jìn)行了深入的思考與探究,解答如下: 解:過點(diǎn)E,F(xiàn)作⊙O,使其與直線l相切,切點(diǎn)為P.在直線l上任取一點(diǎn)Q(異于點(diǎn)P),連接EQ交⊙O于點(diǎn)H,連接FQ,F(xiàn)H, 則∠EPF=∠EHF.(依據(jù)1) ∵∠EHF=∠EQF+∠HFQ,(依據(jù)2) ∴∠EHF>∠EQF, ∴∠EPF>∠EQF. 故當(dāng)球員在點(diǎn)P處射門時(shí),進(jìn)球的可能性最大. |
(1)上面的證明過程中“依據(jù)1”和“依據(jù)2”分別是指:
依據(jù)1:
同弧所對(duì)的圓周角相等
同弧所對(duì)的圓周角相等
.依據(jù)2:
三角形的外角等于和它不相鄰的兩個(gè)內(nèi)角的和
三角形的外角等于和它不相鄰的兩個(gè)內(nèi)角的和
.(2)如圖(3),已知足球球門寬EF為
3
2
3
2

【考點(diǎn)】圓的綜合題.
【答案】同弧所對(duì)的圓周角相等;三角形的外角等于和它不相鄰的兩個(gè)內(nèi)角的和
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:188引用:1難度:0.5
相似題
-
1.如圖1,以點(diǎn)O為圓心,半徑為4的圓交x軸于A,B兩點(diǎn),交y軸于C,D兩點(diǎn),點(diǎn)P為劣弧AC上的一動(dòng)點(diǎn),延長CP交x軸于點(diǎn)E;連接PB,交OC于點(diǎn)F.
(1)若點(diǎn)F為OC的中點(diǎn),求PB的長;
(2)求CP?CE的值;
(3)如圖2,過點(diǎn)O作OH∥AP交PD于點(diǎn)H,當(dāng)點(diǎn)P在弧AC上運(yùn)動(dòng)時(shí),連接AC,PC.試問△APC與△OHD相似嗎?說明理由;的值是否保持不變?若不變,試證明,求出它的值;若發(fā)生變化,請(qǐng)說明理由.APDH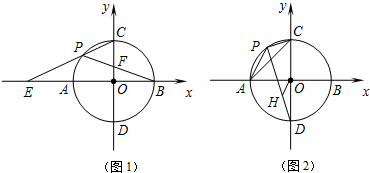 發(fā)布:2025/6/24 18:30:1組卷:272引用:1難度:0.5
發(fā)布:2025/6/24 18:30:1組卷:272引用:1難度:0.5 -
2.下面是“用三角板畫圓的切線”的畫圖過程.
如圖1,已知圓上一點(diǎn)A,畫過A點(diǎn)的圓的切線.畫法:
(1)如圖2,將三角板的直角頂點(diǎn)放在圓上任一點(diǎn)C(與點(diǎn)A不重合)處,使其一直角邊經(jīng)過點(diǎn)A,另一條直角邊與圓交于B點(diǎn),連接AB;
(2)如圖3,將三角板的直角頂點(diǎn)與點(diǎn)A重合,使一條直角邊經(jīng)過點(diǎn)B,畫出另一條直角邊所在的直線AD.則直線AD就是過點(diǎn)A的圓的切線.
請(qǐng)回答:①這種畫法是否正確 (是或否);
②你判斷的依據(jù)是:.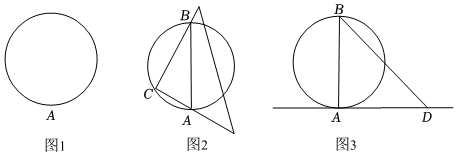 發(fā)布:2025/6/25 8:0:1組卷:19引用:1難度:0.4
發(fā)布:2025/6/25 8:0:1組卷:19引用:1難度:0.4 -
 3.如圖,已知⊙O′與x軸交于A、B兩點(diǎn),與y軸交于C、D兩點(diǎn),圓心O′的坐標(biāo)是(1,-1),半徑為.5
3.如圖,已知⊙O′與x軸交于A、B兩點(diǎn),與y軸交于C、D兩點(diǎn),圓心O′的坐標(biāo)是(1,-1),半徑為.5
(1)比較線段AB與CD的大小;
(2)求A、B、C、D四點(diǎn)的坐標(biāo);
(3)過點(diǎn)D作⊙O′的切線,試求這條切線的解析式.發(fā)布:2025/6/24 20:0:2組卷:43引用:1難度:0.5


