問題:如何快速計算1+2+3+…+n的值呢?
(1)探究:令s=1+2+3+…+n①,
則s=n+(n-1)+(n-2)+…+1②
①+②得2s=(n+1)+(n+1)+…+(n+1)
=n(n+1)
因此s=n(n+1)2n(n+1)2.
(2)應用:
①計算:1+2+3+…+200=2010020100;
②如圖1,一串連續的整數1,2,3,4,…自上往下排列,最上面一行有一個數,以下各行均比上一行多一個數字,若共有15行數字,則最底下一行最左邊的數是106106;
③如圖2,一串連續的基數-25,-24,-23,…按圖1方式排列,共有14行數字,求圖2中所有數字的和.
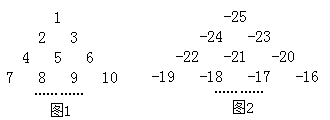
n
(
n
+
1
)
2
n
(
n
+
1
)
2
【考點】規律型:數字的變化類;合并同類項.
【答案】;20100;106
n
(
n
+
1
)
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:221引用:3難度:0.5
相似題
-
1.若x是不等于1的數,我們把
稱為x的差倒數,如2的差倒數是11-x=-1,-1的差倒數是11-2=11-(-1).現已知x1=-12,x2是x1的差倒數,x3是x2的差倒數,x4是x3的差倒數…以此類推,則x2022=.13發布:2025/6/16 22:0:2組卷:189引用:4難度:0.7 -
2.觀察下列算式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,…,根據上述算式中的規律,你認為31+32+33+…+32020+32021的末位數字是 .
發布:2025/6/16 23:30:1組卷:293引用:2難度:0.5 -
3.已知123456789101112…997998999是由連續整數1至999排列組成的一個數,在該數中從左往右數第2022位上的數字為 .
發布:2025/6/16 19:0:1組卷:24引用:1難度:0.7


