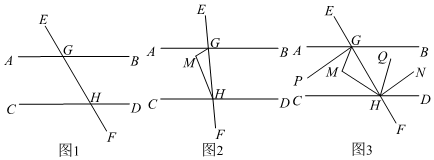
已知，直線EF分別與直線AB、CD相交于點G、H，并且∠AGE+∠DHE=180°．
（1）如圖1，求證：AB∥CD．
（2）如圖2，點M在直線AB、CD之間，連接MG、HM，當∠AGM=32°，∠MHC=68°時，求∠GMH的度數(shù)．
（3）只保持（2）中所求∠GMH的度數(shù)不變，如圖3，GP是∠AGM的平分線，HQ是∠MHD的平分線，作HN∥PG，則∠QHN的度數(shù)是否改變？若不發(fā)生改變，請求出它的度數(shù)．若發(fā)生改變，請說明理由．（本題中的角均為大于0°且小于180°的角）
【考點】平行線的判定與性質(zhì)．
【答案】（1）證明過程見解析；（2）∠GMH=100°；（3）∠QHN=40°．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/5 23:0:2組卷：1780引用：4難度：0.3
相似題
-
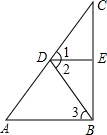1．如圖，∠1=∠2，DE⊥BC，AB⊥BC，那么∠A=∠3嗎？說明理由．
解：∠A=∠3，理由如下：
∵DE⊥BC，AB⊥BC（已知）
∴∠DEB=∠ABC=90°（）
∴∠DEB+（）=180°
∴DE∥AB（）
∴∠1=∠A（）
∠2=∠3（）
∵∠1=∠2（已知）
∴∠A=∠3（）發(fā)布：2025/6/8 19:0:1組卷：304引用：9難度：0.5 -
2．已知的三角形的三個內(nèi)角的度數(shù)和是180°，如圖是兩個三角板不同位置的擺放，其中∠ACB=∠CDE=90°，∠BAC=60°，∠DEC=45°．
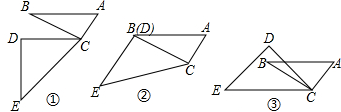
（1）當AB∥DC時，如圖①，求∠DCB的度數(shù)．
（2）當CD與CB重合時，如圖②，判斷DE與AC的位置關(guān)系，并說明理由．
（3）如圖③，當∠DCB等于度時，AB∥EC．發(fā)布：2025/6/8 19:0:1組卷：172引用：4難度：0.5 -
3．將一副三角板按如圖放置，則下列結(jié)論：
①∠1=∠3；②如果∠2=30°，則有AC∥DE；③∠2+∠CAD=180°；④如果∠4=∠C，必有AB⊥ED．其中正確的有 （填寫序號）發(fā)布：2025/6/8 19:0:1組卷：354引用：6難度：0.7