已知直線MN∥PQ，點A在直線MN上，點B，C為平面內兩點，AC⊥BC于點C．
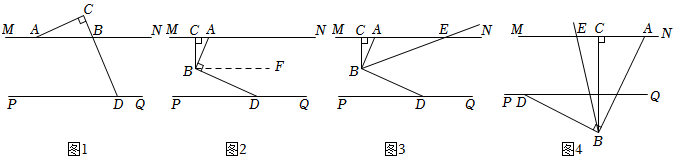
（1）如圖1，當點B在直線MN上，點C在直線MN上方時，延長CB交直線PQ于點D，則∠CAB和∠CDP之間的數量關系是 ∠CAB+∠CDP=90°∠CAB+∠CDP=90°；
（2）如圖2，當點C在直線MN上且在點A左側，點B在直線MN與PQ之間時，過點B作BD⊥AB交直線PQ于點D．為探究∠ABC與∠BDP之間的數量關系，小明過點B作BF∥MN請根據他的思路，寫出∠ABC與∠BDP的關系，并說明理由；
（3）請從下面A，B兩題中任選一題作答．A．如圖3，在（2）的條件下，作∠ABD的平分線交直線MN于點E，當∠AEB=2∠ABC時直接寫出∠ABC的度數；B．如圖4，當點C在直線MN上且在點A左側，點B在直線PQ下方時，過點B作BD⊥AB交直線PQ于點D，作∠ABD的平分線交直線MN于點E，當∠BDP=2∠BEN時，直接寫出∠ABC的度數．
【考點】平行線的判定與性質．
【答案】∠CAB+∠CDP=90°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 23:0:1組卷：650引用：2難度：0.7
相似題
-
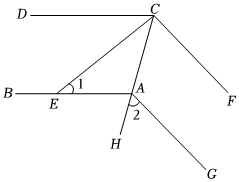1．如圖，AB∥CD，CE平分∠ACD，CF⊥CE，∠1=35°，
（1）求∠ACE的度數；
（2）若∠2=55°，求證：CF∥AG．發布：2025/6/7 23:30:2組卷：105引用：4難度：0.7 -
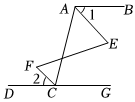2．完成下面的推理過程．已知：如圖，∠BAC與∠GCA互補，∠1=∠2，求證：∠E=∠F．
證明：∵∠BAC與∠GCA互補．
即 ，
∴AB∥DG（ ）．
∴∠BAC=∠ACD．（ ）．
又∵∠1=∠2，（已知）．
∴∠BAC-∠1=∠ACD-∠2，即∠EAC=∠FCA．（ ）．
∴∥（內錯角相等，兩直線平行）．
∴∠E=∠F．（ ）．發布：2025/6/7 23:30:2組卷：90引用：1難度：0.6 -
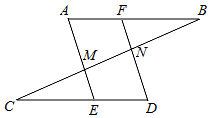3．如圖，AB∥CD，∠A=∠D，有下列結論：①∠B=∠C；②AE∥DF；③AE⊥BC；④∠AMC=∠BND．其中正確的有．（只填序號）發布：2025/6/7 23:30:2組卷：363引用：5難度：0.7