如圖，在正方形ABCD中，E、F是對(duì)角線BD上兩點(diǎn)，且∠EAF=45°，將△ADF繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90°后，得到△ABQ，連接EQ，求證：
（1）EA是∠QED的平分線；
（2）EF²=BE²+DF²．

【答案】見試題解答內(nèi)容

【解答】

【點(diǎn)評(píng)】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2024/6/27 10:35:59組卷：6514引用：32難度：0.3

相似題

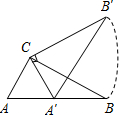1．三角板ABC中，∠ACB=90°，∠B=30°，AC=2
3
，三角板繞直角頂點(diǎn)C逆時(shí)針旋轉(zhuǎn)，當(dāng)點(diǎn)A的對(duì)應(yīng)點(diǎn)A′落在AB邊的起始位置上時(shí)即停止轉(zhuǎn)動(dòng)，則B點(diǎn)轉(zhuǎn)過的路徑長(zhǎng)為（　　）
A．
3
2
π B．
4
3
3
π C．2π D．3π
發(fā)布：2025/5/21 20:0:2組卷：623引用：9難度：0.9
解析
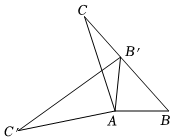2．如圖，在△ABC中，∠BAC=108°，將△ABC繞點(diǎn)A按逆時(shí)針方向旋轉(zhuǎn)得到△A'B'C'，若點(diǎn)B'恰好落在BC邊上，且AB'=CB'，則∠C'的大小為（　　）
A．20° B．24° C．28° D．32°
發(fā)布：2025/5/21 20:30:1組卷：90引用：4難度：0.5
解析
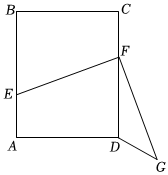3．如圖，矩形ABCD中，AB=6，BC=4，點(diǎn)E，F(xiàn)分別為邊AB，CD上的動(dòng)點(diǎn)，且AE=CF，將線段EF繞點(diǎn)F逆時(shí)針旋轉(zhuǎn)90°得到線段FG，連接DG．
（1）當(dāng)點(diǎn)E為AB的中點(diǎn)時(shí)，線段DG的長(zhǎng)是
；
（2）當(dāng)點(diǎn)E在邊AB上運(yùn)動(dòng)時(shí)，線段DG的最小值是
．
發(fā)布：2025/5/21 20:30:1組卷：1344引用：4難度：0.3
解析

相關(guān)試卷

如圖，在正方形ABCD中，E、F是對(duì)角線BD上兩點(diǎn)，且∠EAF=45°，將△ADF繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90°后，得到△ABQ，連接EQ，求證：（1）EA是∠QED的平分線；（2）EF2=BE2+DF2．