某數學學習小組在學習了相似三角形以后，他們發現對于同一個物體在燈光下，它的影子的長度與電燈到物體的距離有一定的關系，利用物體影子的長度可以計算電燈到物體的距離，利用電燈到物體的距離也可以計算物體影子的長度．下面是他們的試驗內容，請解答：
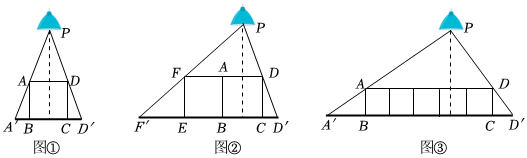
（1）如圖①，放在水平地面上的正方形框架ABCD，在其正上方有一個小射燈P，在小射燈P的照射下，正方形框架在地面上的影子為A′B、D′C，若正方形框架的邊長為30cm,A′B=9cm,則△PAD∽△PA′D′PA′D′；小射燈P離地面的距離為 8080cm.
（2）如圖②，不改變圖①中ABCD框架和小射燈P的位置，將另一個同樣大小的小正方形框架緊貼在原小正方形框架的左邊并排擺放，即正方形ABEF．求小射燈下的影長EF'的長度．
（3）如圖③，小射燈P到地面的距離為d,一共有n個邊長為a的小正方形框架（無重疊）并排如圖擺放，影長A′B與CD'的和為 na2d-ana2d-a（用d、n、a表示）．?
n
a
2
d
-
a
n
a
2
d
-
a
【考點】相似形綜合題．
【答案】PA′D′；80；
n
a
2
d
-
a
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/3 15:0:2組卷：513引用：5難度：0.3
相似題
-
1．如圖1，在Rt△ABC中，∠BAC=90°，D為邊AB上一點，∠ACD=∠B．
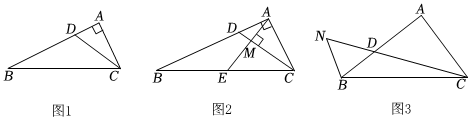
（1）求證：AC2=AD?AB；
（2）如圖2，過點A作AM⊥CD于M，交BC于點E，若AB=4AD，求的值；AMME
（3）如圖，N為CD延長線上一點，連接BN，且∠NBD=2∠ACD，若，直接寫出tan∠ACD=1n（n＞1）的值（用含n的代數式表示）．NDDC發布：2025/5/22 10:30:1組卷：557引用：4難度：0.1 -
2．問題背景：某學習小組正在研究如下問題：如圖1所示，四邊形ABCD與四邊形CEFG均為正方形，且點E、G分別在邊BC、CD上，連接DE、BG，點M是BG中點，連接CM，試猜測CM與DE的數量關系與位置關系，并加以證明．
解決問題：小華從旋轉的角度提出一個問題：如圖2，將正方形CEFG繞點C順時針旋轉一定角度，其他條件不變，此時“問題背景”中的結論還成立嗎？如果成立，請加以證明；如果不成立，請說明理由．
拓展延伸：小剛提出了一個更加一般化的問題：如圖3所示，?ABCD∽?ECGF，且，其他條件不變，此時CM與DE又有怎樣的數量關系？請直接寫出結果．ABBC=ab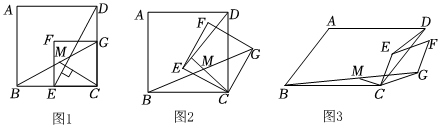
?發布：2025/5/22 10:30:1組卷：242引用：4難度：0.1 -
3．如圖，在Rt△ABC中，∠ACB=90°，AC=6，BC=3．點D是邊AC上一動點（不與A、C重合），聯結BD，過點C作CF⊥BD，分別交BD、AB于點E、F．
（1）當CD=2時，求∠ACF的正切值；
（2）設CD=x,，求y關于x的函數解析式，并寫出x的定義域；AFBF=y
（3）聯結FD并延長，與邊BC的延長線相交于點G，若△DGC與△BAC相似，求的值．AFBF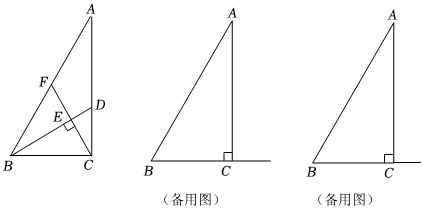
發布：2025/5/22 11:30:2組卷：530引用：1難度：0.4