為了探索代數式x2+1+（8-x）2+25的最小值，
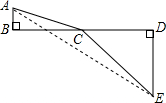
小張巧妙的運用了數學思想．具體方法是這樣的：如圖，C為線段BD上一動點，分別過點B、D作AB⊥BD，ED⊥BD，連接AC、EC．已知AB=1，DE=5，BD=8，設BC=x.則AC=x2+1，CE=（8-x）2+25則問題即轉化成求AC+CE的最小值．
（1）我們知道當A、C、E在同一直線上時，AC+CE的值最小，于是可求得x2+1+（8-x）2+25的最小值等于 1010，此時x=4343；
（2）題中“小張巧妙的運用了數學思想”是指哪種主要的數學思想？
（選填：函數思想，分類討論思想、類比思想、數形結合思想）
（3）請你根據上述的方法和結論，試構圖求出代數式x2+4+（12-x）2+9的最小值 1313．
x
2
+
1
+
（
8
-
x
）
2
+
25
x
2
+
1
（
8
-
x
）
2
+
25
x
2
+
1
+
（
8
-
x
）
2
+
25
4
3
4
3
x
2
+
4
+
（
12
-
x
）
2
+
9
【考點】軸對稱-最短路線問題．
【答案】10；；13
4
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/3 19:0:1組卷：651引用：4難度：0.5
相似題
-
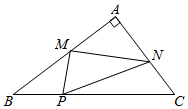1．如圖，在Rt△ABC中，∠A=90°，AB=4，AC=3，M、N、P分別是邊AB、AC、BC上的動點，連接PM、PN和MN，則PM+PN+MN的最小值是 ．發布：2025/5/25 4:0:1組卷：1794引用：4難度：0.3 -
2．如圖，矩形ABCD中，AB=，BC=3，P為矩形內一點，連接PA，PB，PC，則PA+PB+PC的最小值是 ．3發布：2025/5/25 6:30:1組卷：201引用：1難度：0.4 -
3．如圖，在矩形ABCD中，BC=10，∠ABD=30°，若點M、N分別是線段DB、AB上的兩個動點，則AM+MN的最小值為．發布：2025/5/25 5:0:4組卷：2545引用：10難度：0.4