2022-2023學(xué)年廣東省佛山四中八年級(jí)(上)期中數(shù)學(xué)試卷
發(fā)布:2024/10/3 19:0:1
一、單選題(本大題10小題,每小題3分,共30分)在每小題列出的四個(gè)選項(xiàng)中,只有一項(xiàng)是正確的,請(qǐng)把答題卡上對(duì)應(yīng)題目所選的選項(xiàng)涂黑。
-
1.下列實(shí)數(shù)是無(wú)理數(shù)的是( )
A. 13B.0.1010010001 C.π D. 9組卷:271引用:6難度:0.8 -
2.能作為直角三角形的三邊長(zhǎng)的數(shù)據(jù)是( )
A.3,4,6 B.5,12,14 C.1, ,23D. ,2,23組卷:516引用:4難度:0.7 -
3.在平面直角坐標(biāo)系中,點(diǎn)A的坐標(biāo)為(-2,3),則點(diǎn)A關(guān)于y軸對(duì)稱點(diǎn)的坐標(biāo)是( )
A.(-2,-3) B.(-2,3) C.(2,-3) D.(2,3) 組卷:249引用:4難度:0.8 -
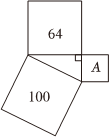 4.若三個(gè)正方形的面積如圖所示,則正方形A的面積為( )
4.若三個(gè)正方形的面積如圖所示,則正方形A的面積為( )A.6 B.36 C.64 D.8 組卷:625引用:14難度:0.9 -
5.如果點(diǎn)P(m+3,m+1)在直角坐標(biāo)系的x軸上,那么P點(diǎn)坐標(biāo)為( )
A.(0,2) B.(2,0) C.(4,0) D.(0,-4) 組卷:996引用:22難度:0.7 -
6.下列等式正確的是( )
A. =-7(-7)2B. =±981C.- =3-82723D. =-3-9組卷:338引用:5難度:0.7 -
7.若b>0,則一次函數(shù)y=-x+b的圖象大致是( )
A. 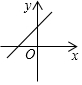
B. 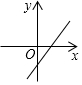
C. 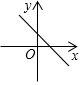
D. 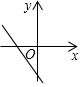 組卷:3861引用:24難度:0.7
組卷:3861引用:24難度:0.7
三、解答題(本大題8小題,18~20題每小題6分,21~23題每小題6分,24~25題每小題6分,共62分)
-
 22.為了探索代數(shù)式的最小值,x2+1+(8-x)2+25
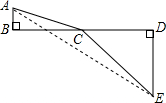
22.為了探索代數(shù)式的最小值,x2+1+(8-x)2+25
小張巧妙的運(yùn)用了數(shù)學(xué)思想.具體方法是這樣的:如圖,C為線段BD上一動(dòng)點(diǎn),分別過(guò)點(diǎn)B、D作AB⊥BD,ED⊥BD,連接AC、EC.已知AB=1,DE=5,BD=8,設(shè)BC=x.則AC=,CE=x2+1則問(wèn)題即轉(zhuǎn)化成求AC+CE的最小值.(8-x)2+25
(1)我們知道當(dāng)A、C、E在同一直線上時(shí),AC+CE的值最小,于是可求得的最小值等于 ,此時(shí)x=;x2+1+(8-x)2+25
(2)題中“小張巧妙的運(yùn)用了數(shù)學(xué)思想”是指哪種主要的數(shù)學(xué)思想?
(選填:函數(shù)思想,分類(lèi)討論思想、類(lèi)比思想、數(shù)形結(jié)合思想)
(3)請(qǐng)你根據(jù)上述的方法和結(jié)論,試構(gòu)圖求出代數(shù)式的最小值 .x2+4+(12-x)2+9組卷:651引用:4難度:0.5 -
 23.在如圖的正方形網(wǎng)格中,每一個(gè)小正方形的邊長(zhǎng)為1,格點(diǎn)三角形ABC(頂點(diǎn)是網(wǎng)格線交點(diǎn)的三角形)的三個(gè)頂點(diǎn)的坐標(biāo)分別為A(1,1),B(4,2),C(3,4).
23.在如圖的正方形網(wǎng)格中,每一個(gè)小正方形的邊長(zhǎng)為1,格點(diǎn)三角形ABC(頂點(diǎn)是網(wǎng)格線交點(diǎn)的三角形)的三個(gè)頂點(diǎn)的坐標(biāo)分別為A(1,1),B(4,2),C(3,4).
(1)請(qǐng)?jiān)趫D中的網(wǎng)格平面內(nèi)建立平面直角坐標(biāo)系,并將△ABC畫(huà)出來(lái).
(2)在圖中找一點(diǎn)D,使AD=,CD=26,并將點(diǎn)D標(biāo)記出來(lái).13
(3)在x軸上找一點(diǎn)P,使PA+PB的值最小,請(qǐng)直接寫(xiě)出點(diǎn)P的坐標(biāo).
(4)在y軸上是否存在點(diǎn)Q,使得S△AOQ=S△ABC,如果存在,求出點(diǎn)Q的坐標(biāo),如果不存在,說(shuō)明理由.12組卷:64引用:2難度:0.5


