2022年陜西省西安市西咸新區灃東新城六中中考數學五模試卷

一、選擇題（本大題共8個小題，每小題3分，共24分。在每個小題給出的四個選項中，只有一項符合題目要求）

• 1．-9的立方根是（　　）

  A．-3

  B．3

  C． 3 - 9

  D． 3 9
  組卷：376引用：4難度：0.8

  解析

• 2．下列四邊形中，對稱軸條數最多的四邊形是（　　）

  A．平行四邊形

  B．等腰梯形

  C．菱形

  D．正方形
  組卷：70引用：2難度：0.9

  解析

• 3．可燃冰，學名叫“天然氣水合物”，是一種高效清潔、儲量巨大的新能源．據報道，僅我國可燃冰預測遠景資源量就超過了1000億噸油當量．將1000億用科學記數法可表示為（　　）

  A．1×103

  B．1×1011

  C．1×1013

  D．1×1014
  組卷：89引用：8難度：0.8

  解析

• 4．計算a⁶÷（-a）³的結果是（　　）

  A．-a3

  B．-a2

  C．a3

  D．a2
  組卷：150引用：3難度：0.7

  解析

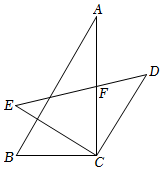• 5．把一副三角板按如圖所示的位置擺放，使直角頂點重合，且CD∥AB，則∠AFD的度數是（　　）

  A．90°

  B．85°

  C．80°

  D．75°
  組卷：75引用：4難度：0.7

  解析

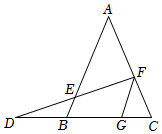• 6．如圖，在△ABC中，AB=AC，D是CB延長線上一點，E是AB上一點，連DE并延長交AC于點F，過F作FG∥AB交BC于點G，若DE=EF，則

  BE

  CF

  的值為（　　）

  A．1

  B． 1 2

  C． 1 3

  D． 2 3
  組卷：577引用：2難度：0.6

  解析

• 7．已知直線的函數表達式為y=kx-3（k≠0），當自變量滿足1≤x≤3時，其對應的函數圖象都在x軸下方，則k的取值范圍是（　　）

  A．k＞3

  B．k＞1

  C．k＜1

  D．k＜3
  組卷：855引用：4難度：0.7

  解析

• 8．已知二次函數y=ax²+bx+c,其函數y與自變量x之間的部分對應值如下表所示，則下列式子：
  

  x	……	-4	- 3 2	- 1 2	1	……
  y	……	- 10 3	5 2	5 2	0	……

  ①abc＞0；
  ②當-3＜x＜1時，y＞0；
  ③4a+2b+c＞0；
  ④關于x的一元二次方程ax²+bx+c=-

  10

  3

  （a≠0）的解是x₁=-4，x₂=3．
  正確的個數是（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：179引用：1難度：0.4

  解析

三、解答題（本大共13個小題，共81分。解答應寫出文字說明、證明過程或演算步驟）

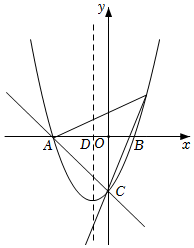• 25．如圖，一次函數y=-x-4的圖象與x軸、y軸分別交于A、C兩點，二次函數y=

  1

  2

  x²+bx+c的圖象經過點A、C，與x軸另一交點為B，其對稱軸交x軸于D．
  （1）求二次函數的表達式．
  （2）在拋物線的對稱軸上是否存在一點N，使得∠ANB=45°．若存在，求出N點坐標，若不存在，請說明理由．
  組卷：410引用：2難度：0.1

  解析

• 26．問題提出：
  （1）如圖1，在矩形ABCD中，AB=4，AD=3，P是對角線AC上的一點，連接PD，將PD繞點P逆時針旋轉90°得到PM，過點M作MN⊥AC于N，求PN的長．
  問題解決：
  （2）2022年3月我省局部發生疫情，為落實“科學防治、精準施策、分級管理”，我省某小區設計防疫區域，在道路CD邊固定柱子（點Q），道路AB邊確定一點P，以PQ為邊，搭建正方形防疫區域PMNQ，內部道路CD上設點E作為記錄處，△EPQ、△EPM、△EMN、△ENQ分別為不同的防疫物資放置區域，設計圖簡化如圖2所示，已知道路兩邊AB∥CD，道路寬為6m,Q為CD上一定點，P為AB上一動點，PE⊥CD于E．請問是否存在符合設計要求且面積最小的△EMN？若存在，請求出面積最小值及此時QE的長；若不存在，請說明理由．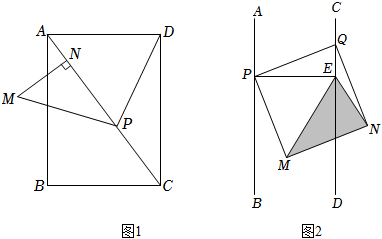
  
  組卷：214引用：2難度：0.1

  解析