如圖，以直角三角形AOC的直角頂點(diǎn)O為原點(diǎn)，以O(shè)C、OA所在直線為x軸和y軸建立平面直角坐標(biāo)系，點(diǎn)A（0，a），C（b,0）滿足a-2b+|b-2|=0．D為線段AC的中點(diǎn)．在平面直角坐標(biāo)系中，以任意兩點(diǎn)P（x1，y1）、Q（x2，y2）為端點(diǎn)的線段中點(diǎn)坐標(biāo)為（x1+x22，y1+y22）．
（1）則A點(diǎn)的坐標(biāo)為（0，4）（0，4）；點(diǎn)C的坐標(biāo)為（2，0）（2，0）．D點(diǎn)的坐標(biāo)為（1，2）（1，2）．
（2）已知坐標(biāo)軸上有兩動(dòng)點(diǎn)P、Q同時(shí)出發(fā)，P點(diǎn)從C點(diǎn)出發(fā)沿x軸負(fù)方向以1個(gè)單位長度每秒的速度勻速移動(dòng)，Q點(diǎn)從O點(diǎn)出發(fā)以2個(gè)單位長度每秒的速度沿y軸正方向移動(dòng)，點(diǎn)Q到達(dá)A點(diǎn)整個(gè)運(yùn)動(dòng)隨之結(jié)束．設(shè)運(yùn)動(dòng)時(shí)間為t（t＞0）秒．問：是否存在這樣的t,使S△ODP=S△ODQ，若存在，請求出t的值；若不存在，請說明理由．
（3）點(diǎn)F是線段AC上一點(diǎn)，滿足∠FOC=∠FCO，點(diǎn)G是第二象限中一點(diǎn)，連OG，使得∠AOG=∠AOF．點(diǎn)E是線段OA上一動(dòng)點(diǎn)，連CE交OF于點(diǎn)H，當(dāng)點(diǎn)E在線段OA上運(yùn)動(dòng)的過程中，∠OHC+∠ACE∠OEC的值是否會(huì)發(fā)生變化？若不變，請求出它的值；若變化，請說明理由．
a
-
2
b
+
|
b
-
2
|
=
0
（
x
1
+
x
2
2
y
1
+
y
2
2
）
∠
OHC
+
∠
ACE
∠
OEC
【考點(diǎn)】三角形綜合題．
【答案】（0，4）；（2，0）；（1，2）
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：1214引用：6難度：0.4
相似題
-
1．在△ABC和△EDC中，∠ACB=∠ECD=90°，BC=k?AC，CD=k?CE．
（1）如圖1，當(dāng)k=1時(shí)，探索AE與BD的關(guān)系；
（2）如圖2，當(dāng)k≠1時(shí)，請?zhí)剿鰽E與BD的關(guān)系，并證明；
（3）如圖3，在（2）的條件下，分別在BD、AE上取點(diǎn)M、N，使得BD=m?MD，AE=m?NE，試探索CN與CM的關(guān)系，并證明．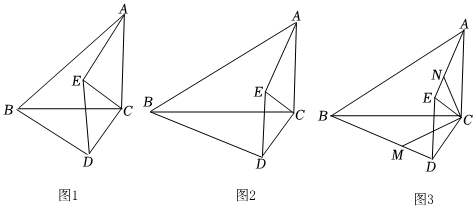
發(fā)布：2025/5/22 16:30:1組卷：88引用：1難度：0.1 -
2．在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，連接CE．
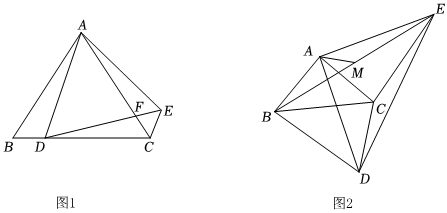
（1）如圖1，若點(diǎn)D在BC邊上，AC，DE相交于F點(diǎn)．
①求證：BD=CE；
②若AF=DF，AB=5，BC=6，求BD的長．
（2）如圖2，若∠BAC=90°，M為BE的中點(diǎn)，連接AM，求證：AM⊥CD．發(fā)布：2025/5/22 16:30:1組卷：211引用：3難度：0.1 -
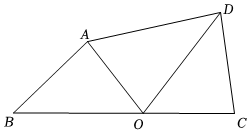3．在四邊形ABCD中，O是邊BC上的一點(diǎn)．若△OAB≌△OCD，則點(diǎn)O叫做該四邊形的“等形點(diǎn)”．
（1）正方形 “等形點(diǎn)”（填“存在”或“不存在”）；
（2）如圖，在四邊形ABCD中，邊BC上的點(diǎn)O是四邊形ABCD的“等形點(diǎn)”．已知CD=4，OA=5，BC=12，連接AC，求AC的長；2
（3）在四邊形EFGH中，EH∥FG．若邊FG上的點(diǎn)O是四邊形EFGH的“等形點(diǎn)”，求的值．OFOG發(fā)布：2025/5/22 14:0:1組卷：2058引用：4難度：0.4