在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，連接CE．
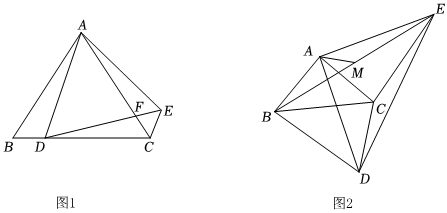
（1）如圖1，若點D在BC邊上，AC，DE相交于F點．
①求證：BD=CE；
②若AF=DF，AB=5，BC=6，求BD的長．
（2）如圖2，若∠BAC=90°，M為BE的中點，連接AM，求證：AM⊥CD．
【考點】三角形綜合題．
【答案】（1）①證明見解答；
②BD=；
（2）證明見解答．
②BD=
11
6
（2）證明見解答．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/22 16:30:1組卷：211引用：3難度：0.1
相似題
-
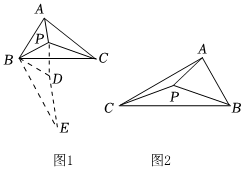1．【閱讀材料】平面幾何中的費馬問題是十七世紀法國數(shù)學家皮埃爾?德?費馬提出的一個著名的幾何問題：給定不在一條直線上的三個點A、B、C，求平面上到這三個點的距離之和最短的點P的位置，費馬問題有多種不同的解法，最簡單快捷的還是幾何解法．如圖1，我們可以將△BPC繞點B順時針旋轉(zhuǎn)60°得到△BDE，連接PD，可得△BPD為等邊三角形，故PD=PB，由旋轉(zhuǎn)可得DE=PC，因PA+PB+PC=PA+PD+DE，由兩點之間線段最短可知，PA+PB+PC的最小值與線段AE的長度相等．
【解決問題】如圖2，在直角三角形ABC內(nèi)部有一動點P，∠BAC=90°，∠ACB=30°，連接PA，PB，PC，若AB=3，求PA+PB+PC的最小值 ．發(fā)布：2025/5/23 11:0:1組卷：400引用：2難度：0.2 -
2．如圖，△ABC是等邊三角形，D是AC的中點，P是BC邊上一動點，且從B以1個單位每秒的速度向C出發(fā)．設(shè)x=BP，y=AP+PD，y關(guān)于x的函數(shù)圖象過點
，則圖象最低點的坐標是 ．（0，6+33）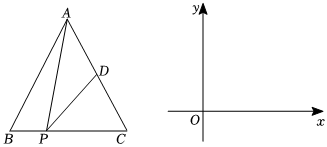
發(fā)布：2025/5/23 11:0:1組卷：182引用：1難度：0.3 -
3．綜合與實踐
問題情境：數(shù)學活動課上，李老師出示了一個問題：
如圖1，在△ABC中，點E，D分別在邊AB，AC上，連接DE，∠ADE=∠ABC，求證：∠AED=∠C．
獨立思考：（1）請解答李老師提出的問題．
實踐探究：（2）在原有問題條件不變的情況下，李老師增加下面的條件，并提出新問題，請你解答．
“如圖2，延長CA至點F，連接BF，使BF=BC，延長DE交BF于點H，點G在AF上，∠FBG=∠ABC，∠FGH=∠BGH，在圖中找出與BE相等的線段，并證明．
問題解決：（3）數(shù)學活動小組同學對上述問題進行特殊化研究之后發(fā)現(xiàn)，當∠BAC=90°時，點G與點A重合，若給出△ABC中任意兩邊長，則圖3中所有已經(jīng)用字母標記的線段長均可求，該小組提出下面的問題，請你解答．
“如圖3，在（2）的條件下，若∠BAC=90°，AB=6，AC=4，求AH的長．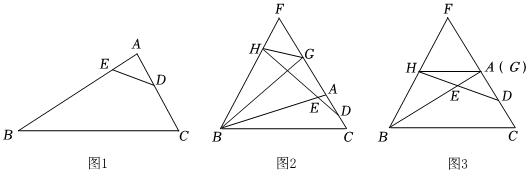
發(fā)布：2025/5/23 11:30:2組卷：512引用：1難度：0.2
相關(guān)試卷